题目内容
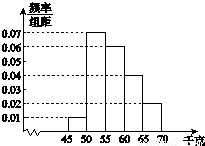
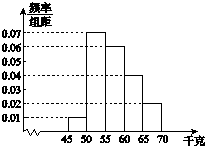 为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图.现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生做初检.
为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图.现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生做初检.(Ⅰ)求每组抽取的学生人数;
(Ⅱ)若从6名学生中再次随机抽取2名学生进行复检,求这2名学生不在同一组的概率.
分析:(I)根据频率分布直方图求出各组学生数之比,再根据分层抽样按比例抽得各组学生数即可;
(II)根据古典概型的计算公式,先求从6名学生抽得2名学生的所有可能情形,再求符合要求的可能情形,根据公式计算即可.
(II)根据古典概型的计算公式,先求从6名学生抽得2名学生的所有可能情形,再求符合要求的可能情形,根据公式计算即可.
解答:解:(Ⅰ)解:由频率分布直方图知,第3,4,5组的学生人数之比为3:2:1.
所以,每组抽取的人数分别为:
第3组:
×6=3;第4组:
×6=2;第5组:
×6=1.
∴从3,4,5组应依次抽取3名学生,2名学生,1名学生.
(Ⅱ)记第3组的3位同学为①,②,③;第4组的2位同学为A,B;第5组的1位同学为C.
则从6位同学中随机抽取2位同学所有可能的情形为:(①,②),(①,③),(①,A),(①,B),(①,C),(②,③),(②,A),(②,B),(②,C),(③,A),
(③,B),(③,C),(A,B),(A,C),(B,C)共15种可能.
其中,(①,②),(①,③),(②,③),(A,B)四种为2名学生在同一组,
∴有11种可能符合2名学生不在同一组的要求,
∴所求概率P=
.
所以,每组抽取的人数分别为:
第3组:
| 3 |
| 6 |
| 2 |
| 6 |
| 1 |
| 6 |
∴从3,4,5组应依次抽取3名学生,2名学生,1名学生.
(Ⅱ)记第3组的3位同学为①,②,③;第4组的2位同学为A,B;第5组的1位同学为C.
则从6位同学中随机抽取2位同学所有可能的情形为:(①,②),(①,③),(①,A),(①,B),(①,C),(②,③),(②,A),(②,B),(②,C),(③,A),
(③,B),(③,C),(A,B),(A,C),(B,C)共15种可能.
其中,(①,②),(①,③),(②,③),(A,B)四种为2名学生在同一组,
∴有11种可能符合2名学生不在同一组的要求,
∴所求概率P=
| 11 |
| 15 |
点评:本题考查频率分布直方图及古典概型的概率计算.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
某学校为了解学生的身体素质情况,对学生进行体能检测,现从1500名学生中随机抽取100名学生进行检测,并把检测结果量化为分数,得下表:
| 得分 | [50,60] | [60,70] | [70,80] | [80,90] | [90,100] |
| 人数 | 5 | 15 | 40 | 30 | 10 |
(2)如果检测分数在85分以上的学生身体素质为良好,估计该学校身体素质良好的学生有多少人;
(3)根据所给数据和“检测分数在85分以上的学生身体素质为良好”的约定,请估计该校学生的总体身体素质状况是否达到良好.
某学校为了解学生的身体素质情况,对学生进行体能检测,现从1500名学生中随机抽取100名学生进行检测,并把检测结果量化为分数,得下表:
(1)绘制检测数据的频率分布直方图;
(2)如果检测分数在85分以上的学生身体素质为良好,估计该学校身体素质良好的学生有多少人;
(3)根据所给数据和“检测分数在85分以上的学生身体素质为良好”的约定,请估计该校学生的总体身体素质状况是否达到良好.
| 得分 | [50,60] | [60,70] | [70,80] | [80,90] | [90,100] |
| 人数 | 5 | 15 | 40 | 30 | 10 |
(2)如果检测分数在85分以上的学生身体素质为良好,估计该学校身体素质良好的学生有多少人;
(3)根据所给数据和“检测分数在85分以上的学生身体素质为良好”的约定,请估计该校学生的总体身体素质状况是否达到良好.