题目内容
某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.(1)求出第4组的频率,并补全频率分布直方图;
(2)如果用分层抽样的方法从“优秀”和“良好”的学生中选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
(3)若该校决定在第4,5 组中随机抽取2名学生接受考官A的面试,第5组中有ξ名学生被考官A面试,求ξ的分布列和数学期望.

【答案】分析:(1)先求出其它组的频率,由此能求出第四组的频率,并能作出频率分布图.
(2)依题意优秀与良好的人数比为3:2,所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人,由此能求出从这5人中选2人至少有1人是优秀的概率.
(3)由频率分布直方图可知,第四组的人数为8人,第五组的人数为4人,ξ的所有可能取值为0,1,2,分别求出其概率,由此能求出ξ的分布列和数学期望.
解答: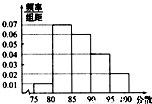 解:(1)其它组的频率为
解:(1)其它组的频率为
(0.01+0.07+0.06+0.02)×5=0.8,
所以第四组的频率为0.2,
频率分布图如图:…(3分)
(2)依题意优秀与良好的人数比为3:2,
所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人,
记从这5人中选2人至少有1人是优秀为事件A,
∴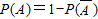 =1-
=1-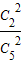 =
= .…(6分)
.…(6分)
(3)由频率分布直方图可知,第四组的人数为8人,第五组的人数为4人,
ξ的所有可能取值为0,1,2,
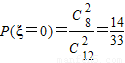 ,
,
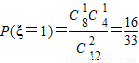 ,
,
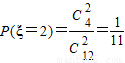 …(9分)
…(9分)
∴ξ的分布列为:
∴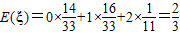 …(12分)
…(12分)
点评:本题考查频率的求法和频率分布直方图的作法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合的知识的合理运用.
(2)依题意优秀与良好的人数比为3:2,所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人,由此能求出从这5人中选2人至少有1人是优秀的概率.
(3)由频率分布直方图可知,第四组的人数为8人,第五组的人数为4人,ξ的所有可能取值为0,1,2,分别求出其概率,由此能求出ξ的分布列和数学期望.
解答:
 解:(1)其它组的频率为
解:(1)其它组的频率为(0.01+0.07+0.06+0.02)×5=0.8,
所以第四组的频率为0.2,
频率分布图如图:…(3分)
(2)依题意优秀与良好的人数比为3:2,
所以采用分层抽样的方法抽取的5人中有优秀3人,良好2人,
记从这5人中选2人至少有1人是优秀为事件A,
∴
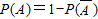 =1-
=1-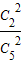 =
= .…(6分)
.…(6分)(3)由频率分布直方图可知,第四组的人数为8人,第五组的人数为4人,
ξ的所有可能取值为0,1,2,
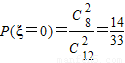 ,
,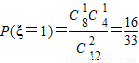 ,
,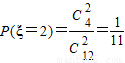 …(9分)
…(9分)∴ξ的分布列为:
| ξ | 1 | 2 | ||
| P | 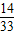 | 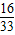 | 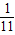 | …(10分) |
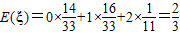 …(12分)
…(12分)点评:本题考查频率的求法和频率分布直方图的作法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合的知识的合理运用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格. (2012•密云县一模)某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,9),
(2012•密云县一模)某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,9), 某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格. (2013•许昌三模)某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成
(2013•许昌三模)某高校在2012年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成 (2013•梅州一模)某高校在2012年的自主招生考试成绩中随机抽以100名学生的笔试成绩,按成绩分组,依次为第一组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185),统计后得到如图所示的频率分布直方图.
(2013•梅州一模)某高校在2012年的自主招生考试成绩中随机抽以100名学生的笔试成绩,按成绩分组,依次为第一组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185),统计后得到如图所示的频率分布直方图.