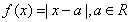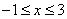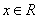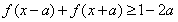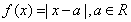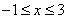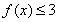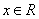摘要：∴当时..对时恒成立对恒成立

网址：http://m.1010jiajiao.com/timu_id_193468[举报]

当p₁，p₂，…，p_n均为正数时，称

为p₁，p₂，…，p_n的“均倒数”．已知数列{a_n}的各项均为正数，且其前n项的“均倒数”为

．
（Ⅰ）试求数列{a_n}的通项公式；
（Ⅱ）设cn=

，试判断并说明c_n+1-c_n（n∈N^*）的符号；
（Ⅲ）已知bn=tan(t＞0)，记数列{b_n}的前n项和为S_n，试求

的值；
（Ⅳ）设函数f(x)=-x2+4x-

，是否存在最大的实数λ，使当x≤λ时，对于一切正整数n，都有f（x）≤0恒成立？查看习题详情和答案>>

当p₁，p₂，…，p_n均为正数时，称

为p₁，p₂，…，p_n的“均倒数”．已知数列{a_n}的各项均为正数，且其前n项的“均倒数”为

．
（1）求数列{a_n}的通项公式；
（2）设cn=

（n∈N^*），试比较c_n+1与c_n的大小；
（3）设函数f(x)=-x2+4x-

，是否存在最大的实数λ，使当x≤λ时，对于一切正整数n，都有f（x）≤0恒成立？

查看习题详情和答案>>

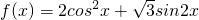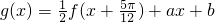设 $数学公式$ ， $数学公式$ ，其中a，b为非零实常数．
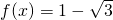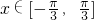（1）若 $数学公式$ ， $数学公式$ ，求x；
（2）若x∈R，试讨论函数g（x）的奇偶性，并证明你的结论；
（3）已知：对于任意x₁，x₂∈R，恒有sin2x₁-sin2x₂≤2（x₁-x₂），当且仅当x₁=x₂时，等号成立．若a≥2，求证：函数g（x）在R上是递增函数．

查看习题详情和答案>>

设

（1）当时，，求a的取值范围；

（2）若对任意，恒成立，求实数a的最小值

查看习题详情和答案>>

设.

（1）当时，，求a的取值范围；

（2）若对任意，恒成立，求实数a的最小值.

查看习题详情和答案>>