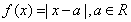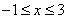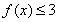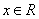题目内容

设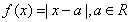

（1）当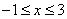时，，求a的取值范围；

（2）若对任意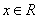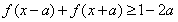，恒成立，求实数a的最小值

 

【答案】

（1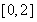）；（2）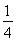

【解析】

试题分析：本题主要考查绝对值不等式的解法、不等式的性质等基础知识，考查学生分析问题解决问题的能力，考查学生的转化能力和计算能力 第一问，利用绝对值不等式的解法，先解出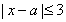的解，再利用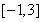是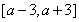的子集，列不等式组，求解；第二问，先利用不等式的性质求出的最小值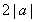，将恒成立的表达式转化为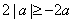，再解绝对值不等式，求出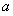的取值范围

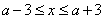试题解析：（1），即 依题意，,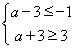

由此得的取值范围是[0，2] 5分

（2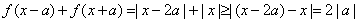） 当且仅当时取等号

解不等式，得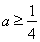

故a的最小值为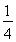 10分

考点：1 绝对值不等式的解法；2 集合的子集关系；3 不等式的性质；4 恒成立问题

 

练习册系列答案
相关题目
设函数f（x）=ax2+bx+c（a，b，c为实数，且a≠0），F(x)=
f(x)
，&x＞0
-f(x)，?x＜0.

（1）若f（-1）=0，曲线y=f（x）通过点（0，2a+3），且在点（-1，f（-1））处的切线垂直于y轴，求F（x）的表达式；
（2）在（Ⅰ）在条件下，当时，，求实数k的取值范围；
（3）设mn＜0，m+n＞0，a＞0，且f（x）为偶函数，证明F（m）+F（n）＞0．
已知m=（x-lnx-y，a），
n
=（
1
x
+lnx+15，1），其中a＞0，且a≠1，当时，y关于x的函数关系式记为y=f（x）；
（1）写出函数f（x）的解析式，并讨论f（x）的单调性；
（2）设函数g（x）=
(-2x3-3ax2-6ax-4a2+6a)   ex，x≤1
e•f(x)，x＞
1（e是自然数的底数）．是否存在正整数a，使g（x）在[-a，a]上为减函数？若存在，求出所有满足条件的正整数a；若不存在，请说明理由．

设函数定义在R上，对于任意实数m、n恒有，且当时，．

(1)求证，且当时，；

(2)求证在R上单调递减；

(3)设集合，集合，若，求a的取值范围．

设.

（1）当时，，求a的取值范围；

（2）若对任意，恒成立，求实数a的最小值.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网