题目内容
设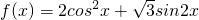 ,
,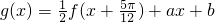 ,其中a,b为非零实常数.
,其中a,b为非零实常数.
(1)若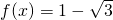 ,
,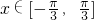 ,求x;
,求x;
(2)若x∈R,试讨论函数g(x)的奇偶性,并证明你的结论;
(3)已知:对于任意x1,x2∈R,恒有sin2x1-sin2x2≤2(x1-x2),当且仅当x1=x2时,等号成立.若a≥2,求证:函数g(x)在R上是递增函数.
解:(1)由已知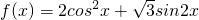 =
=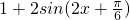 ,(2分)
,(2分)
由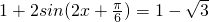 得:
得: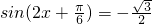 ,(1分)
,(1分)
∵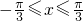 ,
,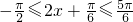 (1分)
(1分)
∴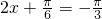 ,
,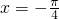 . (1分)
. (1分)
(2)由已知,得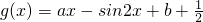 ,(1分)
,(1分)
①∵当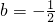 时,对于任意的x∈R,总有g(-x)=-ax-sin(-2x)=-(ax-sin2x)=-g(x),
时,对于任意的x∈R,总有g(-x)=-ax-sin(-2x)=-(ax-sin2x)=-g(x),
∴g(x)是奇函数.(2分)(没有过程扣1分)
②当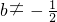 时,∵
时,∵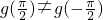 或g(π)≠±g(-π)等
或g(π)≠±g(-π)等
所以,g(x)既不是奇函数,又不是偶函数. (2分)(没有过程扣1分)
(3)对于任意x1,x2∈R,且x1<x2,由已知,有sin2x2-sin2x1<2(x2-x1),(2分)
∴g(x1)-g(x2)=a(x1-x2)+(sin2x2-sin2x1)<(a-2)(x1-x2),
∵a≥2,∴g(x1)-g(x2)<0. (3分)
故,函数g(x)是递增函数. (1分)
注:由于用求导的方法证明不用已知条件,不给分.
分析:(1)由已知中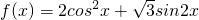 =
=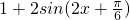 ,根据
,根据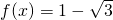 ,
,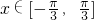 ,我们要以构造一个三角方程,结合正弦函数的图象和性质得到答案.
,我们要以构造一个三角方程,结合正弦函数的图象和性质得到答案.
(2)由已知中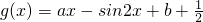 ,根据函数奇偶性的定义及性质,以及正弦型函数的性质,对b的值进行分类讨论,最后综合讨论结果,即可得到结论.
,根据函数奇偶性的定义及性质,以及正弦型函数的性质,对b的值进行分类讨论,最后综合讨论结果,即可得到结论.
(3)由已知中对于任意x1,x2∈R,恒有sin2x1-sin2x2≤2(x1-x2),已知中不应该含绝对值吧,结合已知中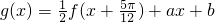 ,利用作差法,易判断出g(x1)-g(x2)<0,进而根据函数单调性的定义,得到结论.
,利用作差法,易判断出g(x1)-g(x2)<0,进而根据函数单调性的定义,得到结论.
点评:本题考查的知识点是三角函数的恒等变换应用,辅助角公式,正弦型函数的图象和性质,函数的奇偶性,函数的单调性,是函数问题比较综合的考查,熟练掌握正弦型函数的图象和性质是解答本题的关键.
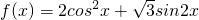 =
=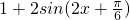 ,(2分)
,(2分)由
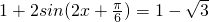 得:
得: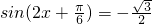 ,(1分)
,(1分)∵
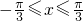 ,
,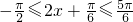 (1分)
(1分)∴
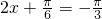 ,
,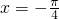 . (1分)
. (1分)(2)由已知,得
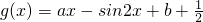 ,(1分)
,(1分)①∵当
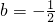 时,对于任意的x∈R,总有g(-x)=-ax-sin(-2x)=-(ax-sin2x)=-g(x),
时,对于任意的x∈R,总有g(-x)=-ax-sin(-2x)=-(ax-sin2x)=-g(x),∴g(x)是奇函数.(2分)(没有过程扣1分)
②当
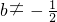 时,∵
时,∵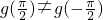 或g(π)≠±g(-π)等
或g(π)≠±g(-π)等所以,g(x)既不是奇函数,又不是偶函数. (2分)(没有过程扣1分)
(3)对于任意x1,x2∈R,且x1<x2,由已知,有sin2x2-sin2x1<2(x2-x1),(2分)
∴g(x1)-g(x2)=a(x1-x2)+(sin2x2-sin2x1)<(a-2)(x1-x2),
∵a≥2,∴g(x1)-g(x2)<0. (3分)
故,函数g(x)是递增函数. (1分)
注:由于用求导的方法证明不用已知条件,不给分.
分析:(1)由已知中
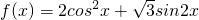 =
=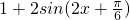 ,根据
,根据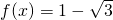 ,
,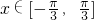 ,我们要以构造一个三角方程,结合正弦函数的图象和性质得到答案.
,我们要以构造一个三角方程,结合正弦函数的图象和性质得到答案.(2)由已知中
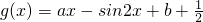 ,根据函数奇偶性的定义及性质,以及正弦型函数的性质,对b的值进行分类讨论,最后综合讨论结果,即可得到结论.
,根据函数奇偶性的定义及性质,以及正弦型函数的性质,对b的值进行分类讨论,最后综合讨论结果,即可得到结论.(3)由已知中对于任意x1,x2∈R,恒有sin2x1-sin2x2≤2(x1-x2),已知中不应该含绝对值吧,结合已知中
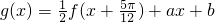 ,利用作差法,易判断出g(x1)-g(x2)<0,进而根据函数单调性的定义,得到结论.
,利用作差法,易判断出g(x1)-g(x2)<0,进而根据函数单调性的定义,得到结论.点评:本题考查的知识点是三角函数的恒等变换应用,辅助角公式,正弦型函数的图象和性质,函数的奇偶性,函数的单调性,是函数问题比较综合的考查,熟练掌握正弦型函数的图象和性质是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目