在定义域上是减函数.求的取值范围,——青夏教育精英家教网—

摘要：在定义域上是减函数.求的取值范围,

网址：http://m.1010jiajiao.com/timu_id_191744[举报]

已知函数y＝f(x)在定义域[－1，1]上是奇函数，又是减函数．

(1)证明对任意的x₁，x₂∈[－1，1]有：[f(x₁)＋f(x₂)](x₁＋x₂)≤0；

(2)若f(1－a)＋f(1－a²)＜0，求实数a的取值范围．

若函数y＝f(x)是偶函数，其定义域为{x|x≠0}，且函数f(x)在(0，＋∞)上是减函数，f(2)＝0，则函数f(x)的零点有 (　　)

A．唯一一个 B．两个

C．至少两个 D．无法判断

设函数y＝f(x)的定义域为R，对任意实数m，n，有f(m＋n)＝f(m)f(n)，且当x＜0时，f(x)＞1数列{a_n}满足a₁＝f(0)，且(n∈N^*)．

(1)求证：y＝f(x)在R上单调递减．

(2)求数列{a_n}的通项公式．

(3)是否存在正数k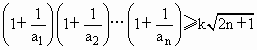，对一切n∈N^*均成立？若存在．试求出k的最大值并证明：若不存在，请说明理由．

已知函数y＝f(x)的定义域是(－∞，＋∞)，考察下列四个结论：

①若，则f(x)是偶函数；

②若，则f(x)在区间[－2，2]上不是减函数；

③若，则方程f(x)＝0在区间(－1，1)内至少有一个实根；

④若R，则f(x)是奇函数或偶函数．

其中正确的是_______．

对于函数y＝f(x)，定义域为D＝[－2，2]．

①若f(－1)＝f(1)，f(－2)＝f(2)，则y＝f(x)是D上的偶函数；

②若对于x∈[－2，2]，都有f(－x)＋f(x)＝0，则y＝f(x)是D上的奇函数；

③若函数y＝f(x)在D上具有单调性且f(0)＞f(1)则y＝f(x)是D上的递减函数；

④若f(－1)＜f(0)＜f(1)＜f(2)，则y＝f(x)是D上的递增函数．

以上命题正确的是________(写出所有正确命题的序号)．

试题分类