题目内容
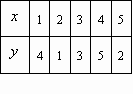
设函数y＝f(x)的定义域为R，对任意实数m，n，有f(m＋n)＝f(m)f(n)，且当x＜0时，f(x)＞1数列{an}满足a1＝f(0)，且
(n∈N*)．
(1)求证：y＝f(x)在R上单调递减．
(2)求数列{an}的通项公式．
(3)是否存在正数k，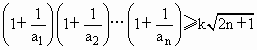
对一切n∈N*均成立？若存在．试求出k的最大值并证明：若不存在，请说明理由．
答案：
解析：
提示：
解析：
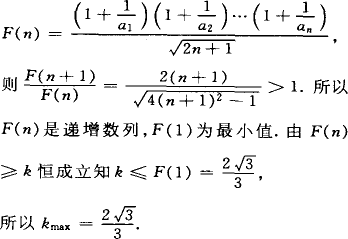
提示：
数列的恒成立问题类似于函数的相关问题，但由于数列的项数为正整数，不具备实数的连续性，有时需验证．
练习册系列答案
阅读快车系列答案
相关题目
)，求数列{an}的前n项和Sn，并求最小的正实数t，使Sn＜tan对任意n∈N
，1)，则y＝f－1(x)的图像必过
，1)
)
－
)＋f(
a
＋a
＋a
＋…＋a
a
＋a
)，Tn为数列{bn}的前n项和，试比较4Sn与Tn的大小.