摘要：综上.直线PQ与x轴垂直时.△PF1Q的面积最大.且最大面积为3. 设△PF1Q内切圆半径为r.则
网址：http://m.1010jiajiao.com/timu_id_183437[举报]
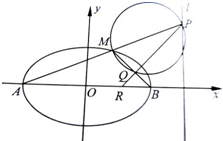如图，A，B是椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
（1）求椭圆C的方程；
（2）设直线AM交l于点P，以MP为直径的圆交直线MB于点Q，试证明：直线PQ与x轴的交点R为定点，并求出R点的坐标．
如图，A，B是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
（I）求椭圆的方程；
（II）设M是椭圆C上异于A，B的一点，直线AM交l于点P，以MP为直径的圆记为⊙k．
（i）若M恰好是椭圆C的上顶点，求⊙k截直线PB所得的弦长；
（ii）设⊙k与直线MB交于点Q，试证明：直线PQ与x轴的交点R为定点，并求该定点的坐标．
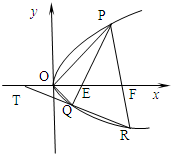设P（x1，y1），Q（x2，y2） 是抛物线C：y2=2px（p＞0）上相异两点，且| OP |
| OQ |
（Ⅰ）若P，Q 到x 轴的距离的积为4，求p的值；
（Ⅱ）若p为已知常数，在x 轴上，是否存在异于E 的一点F，使得直线PF 与抛物线的另一交点为R，而直线RQ 与x 轴相交于T，且有
| TR |
| TQ |
设P（x1，y1），Q（x2，y2） 是抛物线C：y2=2px（p＞0）上相异两点，且
，直线PQ 与x 轴相交于E．
，若存在，求出F 点的坐标（用p 表示），若不存在，说明理由．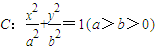
的左右顶点，M是椭圆上异于A，B的任意一点，若椭圆C的离心率为
，且右准线l的方程为x=4．