题目内容
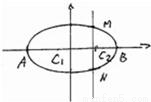
如图,A,B是椭圆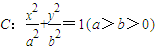 的左右顶点,M是椭圆上异于A,B的任意一点,若椭圆C的离心率为
的左右顶点,M是椭圆上异于A,B的任意一点,若椭圆C的离心率为 ,且右准线l的方程为x=4.
,且右准线l的方程为x=4.(1)求椭圆C的方程;
(2)设直线AM交l于点P,以MP为直径的圆交直线MB于点Q,试证明:直线PQ与x轴的交点R为定点,并求出R点的坐标.

【答案】分析:(1)由椭圆C的离心率为 ,且右准线l的方程为x=4,联立方程组成方程组,即可求得椭圆C的方程;
,且右准线l的方程为x=4,联立方程组成方程组,即可求得椭圆C的方程;
(2)设直线AM的方程,可得点P的坐标,根据MQ⊥PQ,可得kMQ•kPQ=-1,利用M再椭圆上,即可得直线PQ与x轴的交点R为定点.
解答:(1)解:由题意: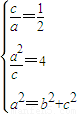 ,解得
,解得 .∴椭圆C的方程为
.∴椭圆C的方程为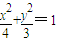 . …(6分)
. …(6分)
(2)证明:由(1)知,A(-2,0),B(2,0),
设M(x,y),R(t,0),则直线AM的方程为 ,
,
令x=4,得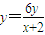 ,即点P的坐标为
,即点P的坐标为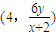 ,…(9分)
,…(9分)
由题意,MQ⊥PQ,∴kMQ•kPQ=-1,∴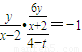 ,即
,即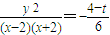 ,…(12分)
,…(12分)
又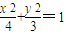 ,∴
,∴ ,∴
,∴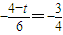 ,∴
,∴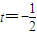 .
.
∴直线PQ与x轴的交点R为定点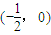 . …(16分)
. …(16分)
点评:本题考查椭圆的标准方程,考查直线过定点,考查学生分析解决问题的能力,属于中档题.
 ,且右准线l的方程为x=4,联立方程组成方程组,即可求得椭圆C的方程;
,且右准线l的方程为x=4,联立方程组成方程组,即可求得椭圆C的方程;(2)设直线AM的方程,可得点P的坐标,根据MQ⊥PQ,可得kMQ•kPQ=-1,利用M再椭圆上,即可得直线PQ与x轴的交点R为定点.
解答:(1)解:由题意:
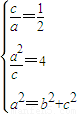 ,解得
,解得 .∴椭圆C的方程为
.∴椭圆C的方程为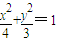 . …(6分)
. …(6分)(2)证明:由(1)知,A(-2,0),B(2,0),
设M(x,y),R(t,0),则直线AM的方程为
 ,
,令x=4,得
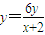 ,即点P的坐标为
,即点P的坐标为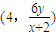 ,…(9分)
,…(9分)由题意,MQ⊥PQ,∴kMQ•kPQ=-1,∴
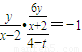 ,即
,即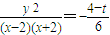 ,…(12分)
,…(12分)又
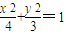 ,∴
,∴ ,∴
,∴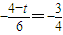 ,∴
,∴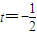 .
.∴直线PQ与x轴的交点R为定点
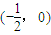 . …(16分)
. …(16分)点评:本题考查椭圆的标准方程,考查直线过定点,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 如图,A,B是椭圆
如图,A,B是椭圆 的左右顶点,M是椭圆上异于A,B的任意一点,若椭圆C的离心率为
的左右顶点,M是椭圆上异于A,B的任意一点,若椭圆C的离心率为 ,且右准线l的方程为x=4.
,且右准线l的方程为x=4.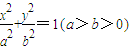 的长轴和短轴端点,点P在椭圆上,F、E是椭圆的左、右焦点,若EP∥AB,PF⊥OF,则该椭圆的离心率等于( )
的长轴和短轴端点,点P在椭圆上,F、E是椭圆的左、右焦点,若EP∥AB,PF⊥OF,则该椭圆的离心率等于( )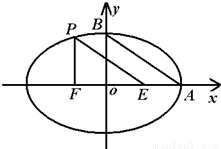
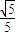

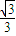

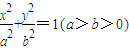 的长轴和短轴端点,点P在椭圆上,F、E是椭圆的左、右焦点,若EP∥AB,PF⊥OF,则该椭圆的离心率等于( )
的长轴和短轴端点,点P在椭圆上,F、E是椭圆的左、右焦点,若EP∥AB,PF⊥OF,则该椭圆的离心率等于( )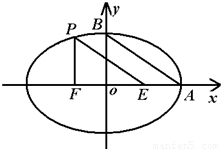
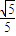

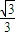

 的左、右顶点,直线x=t(-2<t<2)交椭圆于M、N两点,经过A、M、N的圆的圆心为C1,经过B、M、N的圆的圆心为C2.
的左、右顶点,直线x=t(-2<t<2)交椭圆于M、N两点,经过A、M、N的圆的圆心为C1,经过B、M、N的圆的圆心为C2.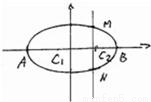
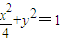 的左、右顶点,直线x=t(-2<t<2)交椭圆于M、N两点,经过A、M、N的圆的圆心为C1,经过B、M、N的圆的圆心为C2.
的左、右顶点,直线x=t(-2<t<2)交椭圆于M、N两点,经过A、M、N的圆的圆心为C1,经过B、M、N的圆的圆心为C2.