题目内容
 如图,A,B是椭圆
如图,A,B是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(I)求椭圆的方程;
(II)设M是椭圆C上异于A,B的一点,直线AM交l于点P,以MP为直径的圆记为⊙k.
(i)若M恰好是椭圆C的上顶点,求⊙k截直线PB所得的弦长;
(ii)设⊙k与直线MB交于点Q,试证明:直线PQ与x轴的交点R为定点,并求该定点的坐标.
分析:(I)由离心率为
,得
=
,由右准线l的方程为x=4,得
=4.再根据b2=a2-c2联立方程组解出即可;
(II)(i)由条件易求直线AM的方程,从而可得P点坐标,进而可求得⊙k的方程,求出圆心到直线PB的距离,利用勾股定理即可求得弦长一半;(ii)设M(x0,y0)(y0≠0),可表示出直线AM的方程,进而表示出P的坐标,由MB⊥PR可求得直线PR的方程,令y=0即可得打点R的横坐标,再根据点M在椭圆上即可求得xR值,从而可证明结论;
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
| a2 |
| c |
(II)(i)由条件易求直线AM的方程,从而可得P点坐标,进而可求得⊙k的方程,求出圆心到直线PB的距离,利用勾股定理即可求得弦长一半;(ii)设M(x0,y0)(y0≠0),可表示出直线AM的方程,进而表示出P的坐标,由MB⊥PR可求得直线PR的方程,令y=0即可得打点R的横坐标,再根据点M在椭圆上即可求得xR值,从而可证明结论;
解答:解:(I)由题意得,
,解得
,又b2=a2-c2=3,
故所求椭圆的方程为
+
=1;
(II)(i)因为M(0,
),所以直线AM的方程为y=
x+
,
则点P的坐标为P(4,3
),从而⊙k的方程为(x-2)2+(y-2
)2=7,其圆心为(2,2
),半径为
,
又直线PB的方程为3
x-2y-6
=0,
故圆心到直线PB的距离为
,从而截直线PB所得的弦长为2
=
;
(ii)证明:设M(x0,y0)(y0≠0),则直线AM的方程为y=
(x+2),则点P的坐标为P(4,
),
又直线MB的斜率为KMB=
,而MB为直径,所以MB⊥PR,所以KPR=-
,从而直线PR的方程为y-
=-
(x-4),
令y=0,得点R的横坐标为xR=4+
,
又点M在椭圆上,所以
+
=1,即y02=
,故xR=4-6×
=-
,
所以直线PQ与x轴的交点R为定点,且该定点的坐标为(-
,0).
|
|
故所求椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(II)(i)因为M(0,
| 3 |
| ||
| 2 |
| 3 |
则点P的坐标为P(4,3
| 3 |
| 3 |
| 3 |
| 7 |
又直线PB的方程为3
| 3 |
| 3 |
故圆心到直线PB的距离为
4
| ||
|
7-(
|
26
| ||
| 31 |
(ii)证明:设M(x0,y0)(y0≠0),则直线AM的方程为y=
| y0 |
| x0+2 |
| 6y0 |
| x0+2 |
又直线MB的斜率为KMB=
| y0 |
| x0-2 |
| x0-2 |
| y0 |
| 6y0 |
| x0+2 |
| x0-2 |
| y0 |
令y=0,得点R的横坐标为xR=4+
| 6y02 |
| x02-4 |
又点M在椭圆上,所以
| x02 |
| 4 |
| y02 |
| 3 |
| 3(4-x02) |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
所以直线PQ与x轴的交点R为定点,且该定点的坐标为(-
| 1 |
| 2 |
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解及直线方程求法,考查学生综合运用所学知识分析问题解决问题的能力,综合性强,有一定难度.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 已知如图,A、B是椭圆
已知如图,A、B是椭圆 (2013•惠州模拟)如图,A,B是椭圆
(2013•惠州模拟)如图,A,B是椭圆 如图,A,B是椭圆C:
如图,A,B是椭圆C: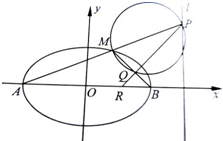 如图,A,B是椭圆
如图,A,B是椭圆