Question

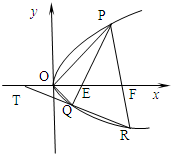设P（x₁，y₁），Q（x₂，y₂） 是抛物线C：y²=2px（p＞0）上相异两点，且

OP

•

OQ

=0，直线PQ 与x 轴相交于E．
（Ⅰ）若P，Q 到x 轴的距离的积为4，求p的值；
（Ⅱ）若p为已知常数，在x 轴上，是否存在异于E 的一点F，使得直线PF 与抛物线的另一交点为R，而直线RQ 与x 轴相交于T，且有

TR

=3

TQ

，若存在，求出F 点的坐标（用p 表示），若不存在，说明理由．

Answer 1

分析：（Ⅰ）由

OP

•

OQ

=0，知x₁x₂+y₁y₂=0，由P、Q在抛物线上，得

y12y22

4p2

+y1y2=0，y₁y₂=-4p²⇒|y₁y₂|=4p²，又|y₁y₂|=4，故得y²=2x，设E（a，0）（a≠0），直线PQ方程为x=my+a，联立方程

x=my+a y2=2px

，得y²-2pmy-2pa=0．由此能导出该抛物线方程及△OPQ的面积的最小值．
（Ⅱ）设E（a，0），直线PQ方程为x=my+a，联立方程组

x=my+a y2=2px

，得y²-2pmy-2pa=0，由此能导出在x轴上，存在异于E的一点F（6p，0），使得

TR

=3

TQ

．

解答：解：（Ⅰ）∵

OP

•

OQ

=0，则x₁x₂+y₁y₂=0，
又P、Q在抛物线上，故y₁²=2px₁，y₂²=2px₂，故得

y12y22

4p2

+y1y2=0，
y₁y₂=-4p²⇒|y₁y₂|=4p²，又|y₁y₂|=4，故得4p²=4，p=1．∴y²=2x，…（4分）
设E（a，0）（a≠0），直线PQ方程为x=my+a，联立方程

x=my+a y2=2px

，
消去x得y²-2pmy-2pa=0；∴y₁y₂=-2pa=-4p²，∴a=2p=2，∴S△OPQ=

1

2

|OE|×(|y1|+|y2|)≥

1

2

×2×2

|y1y2|

=4，∴面积最小值为4．…（6分）
（Ⅱ）设E（a，0），直线PQ方程为x=my+a，联立方程组

x=my+a y2=2px

，
消去x得y²-2pmy-2pa=0；∴y₁y₂=-2pa①
设F（b，0），R（x₃，y₃），同理可知，y₁y₃=-2pb②
由①、②可得

y3

y2

=

b

a

③
若

TR

=3

TQ

，设T（c，0），则有（x₃-c，y₃-0）=3（x₂-c，y₂-0），∴y₃=3y₂即

y3

y2

=3④
将④代入③，得b=3a．又由（Ⅰ）知，

OP

•

OQ

=0，y₁y₂=-4p²，代入①，
可得-2pa=-4p²，a=2p．故b=6p．
故知，在x轴上，存在异于E的一点F（6p，0），使得

TR

=3

TQ

．…（12分）

点评：本题主要考查直线与圆锥曲线的综合应用能力，具体涉及到轨迹方程的求法及直线与抛物线的相关知识，解题时要注意合理地进行等价转化．