摘要:由余弦定理知.
网址:http://m.1010jiajiao.com/timu_id_161088[举报]
(1)用坐标法证明余弦定理:已知在△ABC中,角A、B、C所对的边分别为a、b、c,求证:a2=b2+c2-2bccosA;
(2)在△ABC中,角A、B、C所对的边分别为a、b、c,已知2b=a+c,求角B的最大值;
(3)如果三个正实数a,b,c满足a2=b2+c2-2bccosA,A∈(0,π),那么是否存在以a,b,c为三边的三角形?请说明理由.
查看习题详情和答案>>
(2)在△ABC中,角A、B、C所对的边分别为a、b、c,已知2b=a+c,求角B的最大值;
(3)如果三个正实数a,b,c满足a2=b2+c2-2bccosA,A∈(0,π),那么是否存在以a,b,c为三边的三角形?请说明理由.
(1)用坐标法证明余弦定理:已知在△ABC中,角A、B、C所对的边分别为a、b、c,求证:a2=b2+c2-2bccosA;
(2)在△ABC中,角A、B、C所对的边分别为a、b、c,已知2b=a+c,求角B的最大值;
(3)如果三个正实数a,b,c满足a2=b2+c2-2bccosA,A∈(0,π),那么是否存在以a,b,c为三边的三角形?请说明理由.
查看习题详情和答案>>
(1)用坐标法证明余弦定理:已知在△ABC中,角A、B、C所对的边分别为a、b、c,求证:a2=b2+c2-2bccosA;
(2)在△ABC中,角A、B、C所对的边分别为a、b、c,已知2b=a+c,求角B的最大值;
(3)如果三个正实数a,b,c满足a2=b2+c2-2bccosA,A∈(0,π),那么是否存在以a,b,c为三边的三角形?请说明理由.
查看习题详情和答案>>
(2)在△ABC中,角A、B、C所对的边分别为a、b、c,已知2b=a+c,求角B的最大值;
(3)如果三个正实数a,b,c满足a2=b2+c2-2bccosA,A∈(0,π),那么是否存在以a,b,c为三边的三角形?请说明理由.
 满足
满足 ,试判定
,试判定 ,
,
 ,
, ,
, 是直角三角形.
是直角三角形.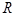 .由正弦定理可得,原式等价于
.由正弦定理可得,原式等价于

 ,
,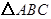 满足
满足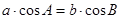 ,试判定
,试判定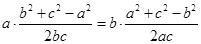 ,
,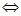
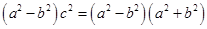 ,
,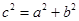 ,
,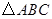 是直角三角形.
是直角三角形.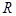 .由正弦定理可得,原式等价于
.由正弦定理可得,原式等价于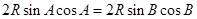
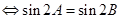
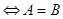 ,
,