题目内容
(1)用坐标法证明余弦定理:已知在△ABC中,角A、B、C所对的边分别为a、b、c,求证:a2=b2+c2-2bccosA;
(2)在△ABC中,角A、B、C所对的边分别为a、b、c,已知2b=a+c,求角B的最大值;
(3)如果三个正实数a,b,c满足a2=b2+c2-2bccosA,A∈(0,π),那么是否存在以a,b,c为三边的三角形?请说明理由.
解:(1)以A为坐标原点,AB所在直线为x轴,AB的垂线为y轴,建立平面直角坐标系,则C(bcosA,bsinA),B(c,0)
∴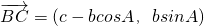
∴a2=(c-bcosA)2+(bsinA)2=b2+c2-2bccosA;
(2)由2b=a+c,得到b= ,
,
则cosB= =
=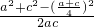
=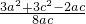 ≥
≥ =
= ,
,
由B∈(0,180°),cosB为减函数,
所以内角B的最大值为60°.
(3)不妨假设不存在以a,b,c为三边的三角形,即 c+b<a
∴c2+b2+2cb<b2+c2-2bccosA
∴cosA<-1
∵A∈(0,π),
∴矛盾
故假设不成立,即存在以a,b,c为三边的三角形
分析:(1)以A为坐标原点,AB所在直线为x轴,AB的垂线为y轴,建立平面直角坐标系,则C(bcosA,bsinA),B(c,0),由此可证余弦定理;
(2)由已知的等式表示出b,然后利用余弦定理表示出cosB,把表示的b代入利用基本不等式即可求出cosB的最大值,由B的范围及余弦函数在此范围内为减函数,即可得到角B的最大值.
(3)用反证法证明.假设不存在以a,b,c为三边的三角形,即 c+b<a,两边平方,再代入条件,引出矛盾,从而得证.
点评:本题以三角形为载体,考查学生灵活运用余弦定理化简求值,掌握余弦函数的图象和性质,是一道中档题.
∴
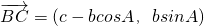
∴a2=(c-bcosA)2+(bsinA)2=b2+c2-2bccosA;
(2)由2b=a+c,得到b=
 ,
,则cosB=
 =
=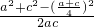
=
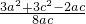 ≥
≥ =
= ,
,由B∈(0,180°),cosB为减函数,
所以内角B的最大值为60°.
(3)不妨假设不存在以a,b,c为三边的三角形,即 c+b<a
∴c2+b2+2cb<b2+c2-2bccosA
∴cosA<-1
∵A∈(0,π),
∴矛盾
故假设不成立,即存在以a,b,c为三边的三角形
分析:(1)以A为坐标原点,AB所在直线为x轴,AB的垂线为y轴,建立平面直角坐标系,则C(bcosA,bsinA),B(c,0),由此可证余弦定理;
(2)由已知的等式表示出b,然后利用余弦定理表示出cosB,把表示的b代入利用基本不等式即可求出cosB的最大值,由B的范围及余弦函数在此范围内为减函数,即可得到角B的最大值.
(3)用反证法证明.假设不存在以a,b,c为三边的三角形,即 c+b<a,两边平方,再代入条件,引出矛盾,从而得证.
点评:本题以三角形为载体,考查学生灵活运用余弦定理化简求值,掌握余弦函数的图象和性质,是一道中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目