（06年广东卷）（14分）

已知公比为的无穷等比数列各项的和为9，无穷等比数列各项的和为.

(Ⅰ)求数列的首项和公比；

(Ⅱ)对给定的,设是首项为，公差为的等差数列.求数列的前10项之和；

(Ⅲ)设为数列的第项，，求，并求正整数，使得

存在且不等于零.

(注：无穷等比数列各项的和即当时该无穷数列前n项和的极限)

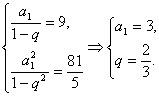(1)求数列{a_n}的首项a₁和公比q;

(2)对给定的k(k=1,2,…,n)，设T^(k)是首项为a_k，公差为2a_k-1的等差数列，求数列T⁽²⁾的前10项之和；

(3)设bⁱ为数列T⁽ⁱ⁾的第i项，S_n=b₁+b₂+…+b_n，求S_n，并求正整数m(m＞1)，使得存在且不等于零.

(注：无穷等比数列各项的和即当n→∞时该无穷等比数列前n项和的极限)

已知公比为q(0＜q＜1)的无穷等比数列{a_n}各项的和为9，无穷等比数列{a_n²}各项的和为。

（Ⅰ）求数列{a_n}的首项a₁和公比q：

（Ⅱ）对给定的k(k=1,2,…,n),设T{k}是首项为a_k，公差为2a_k-1的等差数列，求数列T{2}的前10项之和：

（Ⅲ）设b_i为数列的第i项，s_n=b₁+b₂+…+b_n，求s_n，并求正整数m(m＞1),使得存在且不等于零。

（注：无穷等比数列各项的和即当n时该无穷等比数列前n项和的极限）

(Ⅰ)证明{b_n}为等比数列；

（Ⅱ）如果无穷等比数列{b_n}各项的和S=,求数列{a_n}的首项a₁和公差d.

(注：无穷数列各项的和即当n→∞时数列前n项和的极限)

已知{a_n}是各项均为正数的等差数列，lga₁、lga₂、lga₄成等差数列，又b_n=,n=1,2,3….

(Ⅰ)证明{b_n}为等比数列；

(Ⅱ）如果无穷等比数列{b_n}各项的和S=,求数列{a_n}的首项a₁和公差d.

(注：无穷数列各项的和即当n→∞时数列前n项和的极限)