题目内容
（06年广东卷）（14分）
已知公比为
的无穷等比数列
各项的和为9，无穷等比数列
各项的和为
.
(Ⅰ)求数列的首项
和公比
；
(Ⅱ)对给定的
,设
是首项为
，公差为
的等差数列.求数列的前10项之和；
(Ⅲ)设
为数列
的第
项，
，求
，并求正整数
，使得
存在且不等于零.
(注：无穷等比数列各项的和即当
时该无穷数列前n项和的极限)
解析：(Ⅰ)依题意可知,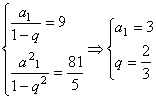
(Ⅱ)由(Ⅰ)知,
,所以数列
的的首项为
,公差
,
,即数列的前10项之和为155.
(Ⅲ) 
=
=
=
，
，
=
当m=2时，=－
，当m>2时，=0，所以m=2
练习册系列答案
相关题目
,则双曲线右支上的点P到右焦点的距离与点P到右准线的距离之比等于
B.
C. 2 D.4
的最小正周期；
，求
的值.