题目内容
(18)已知{an}是各项均为正数的等差数列,lga1、lga2、lga4成等差数列,又bn=(Ⅰ)证明{bn}为等比数列;
(Ⅱ)如果无穷等比数列{bn}各项的和S=![]() ,求数列{an}的首项a1和公差d.
,求数列{an}的首项a1和公差d.
(注:无穷数列各项的和即当n→∞时数列前n项和的极限)
(18)(Ⅰ)证明:
∵lga1、lga2、lga4成等差数列,
∴2lga2=lga1+lga4,即a2=a1·a4.
等差数列{an}的公差为d,则
(a1+d)2=a1(a1+3d),
这样d2=a1d.
从而d(d-a1)=0.
(i)若d=0,则{an}为常数列,相应{bn}也是常数列.
此时{bn}是首项为正数,公式为1的等比数列.
(ii)若d=a1≠0,则
![]() =a1+(2n-1)d=2nd,bn=
=a1+(2n-1)d=2nd,bn=![]() .
.
这时{bn}是首项b1=![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
综上知,{bn}为等比数列.
(Ⅱ)解:
如果无穷等比数列{bn}的公比q=1,则当n→∞时其前n项和的极限不存在.
因而d=a1≠0,这时公比q=![]() ,b1=
,b1=![]() .
.
这样,{bn}的前n项和Sn=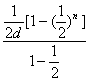 ,
,
则S=![]() Sn=
Sn=![]()
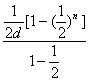 =
=![]() .
.
由S=![]() 得公差d=3,首项a1=d=3.
得公差d=3,首项a1=d=3.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目