网址：http://m.1010jiajiao.com/timu_id_154835[举报]
一、选择题
ACADB BBCAB
二、填空题
11．1 12．－6 13．0 14．4 15．450 16．31030
三、解答题：
17．（1）恰有3个红球的概率为
…………5分
（2）停止摸球时，已知摸到红球次数为三次记为事件B
则事件B发生所摸球的次数为3次 4次或5次 …………8分
所以
…………12分
18．解：设
…………2分
即
…………4分
（1）当
时
…………8分
（2）当
上是增函数，
所以
故
…………12分
19．解：（I）依题意
…………3分
故
上是减函数
即
……………6分
（II）由（I）知
上的减函数，
又
…………9分
故
因此，存在实数m，使得命p且q为真命题，且m的取值范围为
…………12分
20．解：（1）
， …………2分
由题知：
； …………6分
（2）由（1）知：
， …………8分
恒成立，
所以：
…………12分
21．解：（1）
上，
， …………1分
为首项，公差为1的等差数列，
…………4分
当
，
…………6分
证明：（II）
，…………8分
，
…………14分
22．解：（I）函数
内是奇函数等价于
对任意
…………2分
即
，…………4分
因为
，
即
， …………6分
此式对任意
，
所以得b的取值范围是
…………8分
（II）设任意的
，
得
， …………10分
所以
， …………12分
从而
，
因此
内是减函数，具有单调性。 …………14分
| 1 |
| 3 |
| a+1 |
| 2 |
（Ⅰ） 当a=2时，求f （x）的极小值；
（Ⅱ） 若函数g（x）=4x3+3bx2-6（b+2）x （b∈R） 的极小值点与f （x）的极小值点相同，求证：g（x）的极大值小于等于10． 查看习题详情和答案>>
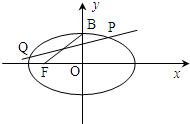已知椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
（1）设椭圆的半焦距c=1，且a2，b2，c2成等差数列，求椭圆C的方程；
（2）对（1）中的椭圆C，直线y=x+1与C交于P、Q两点，求|PQ|的值；
（3）设B为椭圆C：
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
| π |
| 4 |
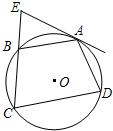A．如图，四边形ABCD内接于⊙O，弧AB=弧AD，过A点的切线交CB的延长线于E点．