题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)设椭圆的半焦距c=1,且a2,b2,c2成等差数列,求椭圆C的方程;
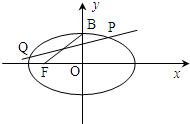
(2)对(1)中的椭圆C,直线y=x+1与C交于P、Q两点,求|PQ|的值;
(3)设B为椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
| π |
| 4 |
分析:(1)直接根据条件列出关于a2,b2,c2的方程,求出a2,b2,c2即可得到椭圆方程;
(2)把直线方程与椭圆方程联立得到关于P、Q两点坐标之间的关系,再结合两点间的距离公式即可求|PQ|的值;
(3)先根据①知
≤
≤
,再结合②整理去掉b即可求出椭圆长轴的取值范围(注意长轴的长是指2a).
(2)把直线方程与椭圆方程联立得到关于P、Q两点坐标之间的关系,再结合两点间的距离公式即可求|PQ|的值;
(3)先根据①知
| 1 |
| 2 |
| b |
| a |
| ||
| 2 |
解答:(本题满分(16分),第1题(4分),第2题(6分),第3题6分)
解:(1)由已知,a2=b2+1,且2b2=a2+1,…(2分)
解得a2=3,b2=2,所以椭圆C的方程是
+
=1.…(4分)
(2)将y=x+1代入椭圆C的方程,得
+
=1,化简得,5x2+6x-3=0,
设P(x1,y1),Q(x2,y2),则x1+x2=-
,x1x2=-
,…(6分)
所以,|PQ|2=(x1-x2)2+(y1-y2)2=2(x1-x2)2=2[(x1+x2)2-4x1x2]=2•(
+
)=
,
所以|PQ|=
.…(10分)
(3)由①知,
≤sinθ≤
,即
≤
≤
,…(11分)
由②得,b2=
,而
≤
≤
,即
≤
≤
,…(13分)
解得
≤a≤
,…(15分)
所以,椭圆长轴的取值范围是[
,
].…(16分)
解:(1)由已知,a2=b2+1,且2b2=a2+1,…(2分)
解得a2=3,b2=2,所以椭圆C的方程是
| x2 |
| 3 |
| y2 |
| 2 |
(2)将y=x+1代入椭圆C的方程,得
| x2 |
| 3 |
| (x+1)2 |
| 2 |
设P(x1,y1),Q(x2,y2),则x1+x2=-
| 6 |
| 5 |
| 3 |
| 5 |
所以,|PQ|2=(x1-x2)2+(y1-y2)2=2(x1-x2)2=2[(x1+x2)2-4x1x2]=2•(
| 36 |
| 25 |
| 12 |
| 5 |
| 192 |
| 25 |
所以|PQ|=
8
| ||
| 5 |
(3)由①知,
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| b |
| a |
| ||
| 2 |
由②得,b2=
| a2 |
| 2a2-1 |
| 1 |
| 4 |
| b2 |
| a2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2a2-1 |
| 1 |
| 2 |
解得
| ||
| 2 |
| ||
| 2 |
所以,椭圆长轴的取值范围是[
| 6 |
| 10 |
点评:本题主要考查圆锥曲线与数列,两点间距离公式以及解析几何的综合.

练习册系列答案
相关题目