题目内容
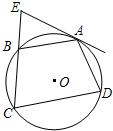 A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点.
A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点.求证:AB2=BE•CD.
B.已知矩阵M
|
C.已知圆的极坐标方程为:ρ2-4
| 2 |
| π |
| 4 |
(1)将圆的极坐标方程化为直角坐标方程;
(2)若点P(x,y)在该圆上,求x+y的最大值和最小值.
D.解不等式|2x-1|<|x|+1.
分析:A:连接AC.因为EA切⊙O于A,所以∠EAB=∠ACB.因为弧AB=弧AD,所以AB=AD.∠EAB=∠ACD.由题设条件推导出△ABE∽△CDA,从而证明出AB2=BE•CD.
B:依题意得由M=
,得|M|=1,故M-1=
,再由矩阵方程能求出点A的坐标.
C:(1)ρ2=x2+y2,ρcosθ=x,ρsinθ=y,转换得x2+y2-4x-4y+6=0.
(2)圆的参数方程为
(α∈R),由此能求出x+y的最大值和最小值.
D:当x<0时,x不存在;当0≤x<
时,解得0<x<
;当x≥
,解得
≤x<2,由此能得到原不等式的解集.
B:依题意得由M=
|
|
C:(1)ρ2=x2+y2,ρcosθ=x,ρsinθ=y,转换得x2+y2-4x-4y+6=0.
(2)圆的参数方程为
|
D:当x<0时,x不存在;当0≤x<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:A 证明:连接AC.
因为EA切⊙O于A,所以∠EAB=∠ACB.
因为弧AB=弧AD,所以∠ACD=∠ACB,AB=AD.
于是∠EAB=∠ACD.
又四边形ABCD内接于⊙O,所以∠ABE=∠D.
所以△ABE∽△CDA.
于是
=
,即AB•DA=BE•CD
所以AB2=BE•CD.
B 解:依题意得
由M=
,得|M|=1,故M-1=
,
从而由
=
得
=
=
=
故
即A(2,-3)为所求.
C 解:(1)ρ2=x2+y2,ρcosθ=x,ρsinθ=y,转换得x2+y2-4x-4y+6=0.
(2)圆的参数方程为
(α∈R),
所以x+y=4+2sin(α+
),那么x+y的最大值为6,最小值为2.
D 解:当x<0时,原不等式可化为-2x+1<-x+1,解得x>0
又∵x<0,∴x不存在;
当0≤x<
时,原不等式可化为-2x+1<x+1,解得x>0
又∵0≤x<
,∴0<x<
;当x≥
,∴
≤x<2
综上,原不等式的解集为{x|0<x<2}.
因为EA切⊙O于A,所以∠EAB=∠ACB.
因为弧AB=弧AD,所以∠ACD=∠ACB,AB=AD.
于是∠EAB=∠ACD.
又四边形ABCD内接于⊙O,所以∠ABE=∠D.
所以△ABE∽△CDA.
于是
| AB |
| CD |
| BE |
| DA |
所以AB2=BE•CD.
B 解:依题意得
由M=
|
|
从而由
|
|
|
|
|
|
|
|
故
|
C 解:(1)ρ2=x2+y2,ρcosθ=x,ρsinθ=y,转换得x2+y2-4x-4y+6=0.
(2)圆的参数方程为
|
所以x+y=4+2sin(α+
| π |
| 4 |
D 解:当x<0时,原不等式可化为-2x+1<-x+1,解得x>0
又∵x<0,∴x不存在;
当0≤x<
| 1 |
| 2 |
又∵0≤x<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上,原不等式的解集为{x|0<x<2}.
点评:本题考查二阶行列式、圆的性质、极坐标和含绝对值的不等式,解题时要注意公式的灵活运用.

练习册系列答案
相关题目
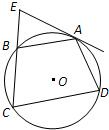 附加题:
附加题: 如图,四边形ABCD中,AB=AD=CD=1,
如图,四边形ABCD中,AB=AD=CD=1, =M
=M ,试求二阶矩阵M.
,试求二阶矩阵M. ,点F1,F2为其左、右焦点,直线l的参数方程为
,点F1,F2为其左、右焦点,直线l的参数方程为 (t为参数,t∈R).求点F1,F2到直线l的距离之和.
(t为参数,t∈R).求点F1,F2到直线l的距离之和. .
.
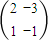 所对应的线性变换把点A(x,y)变成点A′(13,5),试求M的逆矩阵及点A的坐标.
所对应的线性变换把点A(x,y)变成点A′(13,5),试求M的逆矩阵及点A的坐标.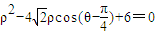 .
.