摘要:.即 (*) , 4分
网址:http://m.1010jiajiao.com/timu_id_13634[举报]
(1)解不等式:
-1>
(2)做一做:
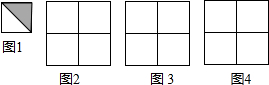
用四块如图1的瓷砖拼成一个正方形,使拼成的图案成轴对称图形,请你在图2,图3,图4中各画出一种拼法(要求三种拼法各不相同,所画图案中的阴影部分用斜线表示)
(3)读一读:
式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和.
由于上述式子比较长,书写也不方便,为了简便起见,我们可以将
“1+2+3+4+5+…+100”表示为
n,这里“Σ”是求和符号.
例如:“1+3+5+7+9+…+99”(即从1开始的100以内的连续奇数的和)可表示为
(2n-1);又如:“13+23+33+43+53+63+73+83+93+103”可表示为
n3.
同学们,通过对以上材料的阅读,请解答下列问题:
<1>2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)用求和符号可表示为 ;
<2>计算:
(n2-1)= (填写最后的计算结果).
查看习题详情和答案>>
| x-3 |
| 2 |
| x-5 |
| 3 |
(2)做一做:

用四块如图1的瓷砖拼成一个正方形,使拼成的图案成轴对称图形,请你在图2,图3,图4中各画出一种拼法(要求三种拼法各不相同,所画图案中的阴影部分用斜线表示)
(3)读一读:
式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和.
由于上述式子比较长,书写也不方便,为了简便起见,我们可以将
“1+2+3+4+5+…+100”表示为
| 100 |
 |
| n=1 |
例如:“1+3+5+7+9+…+99”(即从1开始的100以内的连续奇数的和)可表示为
| 50 |
 |
| n=1 |
| 10 |
 |
| n=1 |
同学们,通过对以上材料的阅读,请解答下列问题:
<1>2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)用求和符号可表示为
<2>计算:
| 5 |
 |
| n=1 |
(如图1),点P将线段AB分成一条较小线段AP和一条较大线段BP,如果
=
,那么称点P为线段AB的黄金分割点,设
=
=k,则k就是黄金比,并且k≈0.618.
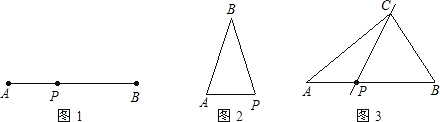
(1)以图1中的AP为底,BP为腰得到等腰△APB(如图2),等腰△APB即为黄金三角形,黄金三角形的定义为:满足
=
≈0.618的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义: ;
(2)如图1,设AB=1,请你说明为什么k约为0.618;
(3)由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果
=
,那么称直线l为该图形的黄金分割线.(如图3),点P是线段AB的黄金分割点,那么直线CP是△ABC的黄金分割线吗?请说明理由;
(4)图3中的△ABC的黄金分割线有几条? 查看习题详情和答案>>
| AP |
| BP |
| BP |
| AB |
| AP |
| BP |
| BP |
| AB |
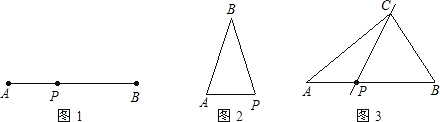
(1)以图1中的AP为底,BP为腰得到等腰△APB(如图2),等腰△APB即为黄金三角形,黄金三角形的定义为:满足
| 底 |
| 腰 |
| 腰 |
| 底+腰 |
(2)如图1,设AB=1,请你说明为什么k约为0.618;
(3)由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果
| S1 |
| S2 |
| S2 |
| S |
(4)图3中的△ABC的黄金分割线有几条? 查看习题详情和答案>>
(1)作图题:(不要求写作法)
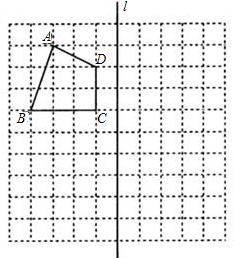
如图,在10×10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上).
①在给出的方格纸中,画出四边形ABCD向下平移5格后的四边形A1B1C1D1;
②在给出的方格纸中,画出四边形ABCD关于直线l对称的图形A2B2C2D2.
(2)某班举行演讲革命故事的比赛中有一个抽奖活动.活动规则是:进入最后决赛的甲、乙两位同学,每人只有一次抽奖机会,在如图所示的翻奖牌正面的4个数字中任选一个数字,选中后可以得到该数字后面的奖品,第一人选中的数字,第二人就不能再选择该数字.
①求第一位抽奖的同学抽中文具与计算器的概率分别是多少?
②有同学认为,如果甲先抽,那么他抽到海宝的概率会大些,你同意这种说法吗?说明理由.
翻奖牌正面:
翻奖牌背面:
查看习题详情和答案>>
如图,在10×10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上).
①在给出的方格纸中,画出四边形ABCD向下平移5格后的四边形A1B1C1D1;
②在给出的方格纸中,画出四边形ABCD关于直线l对称的图形A2B2C2D2.

(2)某班举行演讲革命故事的比赛中有一个抽奖活动.活动规则是:进入最后决赛的甲、乙两位同学,每人只有一次抽奖机会,在如图所示的翻奖牌正面的4个数字中任选一个数字,选中后可以得到该数字后面的奖品,第一人选中的数字,第二人就不能再选择该数字.
①求第一位抽奖的同学抽中文具与计算器的概率分别是多少?
②有同学认为,如果甲先抽,那么他抽到海宝的概率会大些,你同意这种说法吗?说明理由.
翻奖牌正面:
| 1 | 2 |
| 3 | 4 |
| 文具 | 计算器 |
| 计算器 | 海宝 |
24、(1)某校初一(1)、(2)两个班共104人去参观世界珍稀动物展览.每班人数都在60以内,其中(1)班人数较少,不到50人.该展览的门票价格规定:单张票价格为13元;购票人数在51-100人每人门票价为11元;100人以上每人门票价为9元.经估算,如果两班都以班为单位分别购票,则一共应付1240元;如果两班联合起来,作为一个团体购票,则可以节省不少钱.
请问:①两班各有多少名学生?②两班联合起来购票能省多少钱?
(2)甲从学校出发到相距14千米的A地.当到达距学校2千米的B地时发现遗忘某物品.打电话给乙(打电话的时间忽略不计),乙随即从学校出发在C地追上甲后并立即返回.当乙回到学校时甲距A地还有3千米.求学校到C地的距离.
查看习题详情和答案>>
请问:①两班各有多少名学生?②两班联合起来购票能省多少钱?
(2)甲从学校出发到相距14千米的A地.当到达距学校2千米的B地时发现遗忘某物品.打电话给乙(打电话的时间忽略不计),乙随即从学校出发在C地追上甲后并立即返回.当乙回到学校时甲距A地还有3千米.求学校到C地的距离.
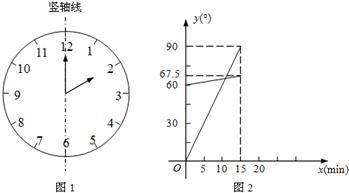
(1)在遇到问题:“钟面上,如果把时针与分针看作是同一平面内的两条线段,在2:00~2:15之间,时针与分针重合的时刻是多少?”时,小明尝试运用建立函数关系的方法:
①恰当选取变量x和y.小明设2点钟之后经过x min(0≤x≤15),时针、分针分别与竖轴线(即经过表示“12”和“6”的点的直线,如图1)所成的角的度数为y1°、y2°;
②确定函数关系.由于时针、分针在单位时间内转动的角度不变,因此既可以直接写出y1、y2关于x的函数关系式,也可以画出它们的图象.小明选择了后者,画出了图2;
③根据题目的要求,利用函数求解.本题中小明认为求出两个图象交点的横坐标就可以解决问题.
请你按照小明的思路解决这个问题.
(2)请运用建立函数关系的方法解决问题:钟面上,如果把时针与分针看作是同一平面内的两条线段,在7:30~8:00之间,时针与分针互相垂直的时刻是多少? 查看习题详情和答案>>
①恰当选取变量x和y.小明设2点钟之后经过x min(0≤x≤15),时针、分针分别与竖轴线(即经过表示“12”和“6”的点的直线,如图1)所成的角的度数为y1°、y2°;
②确定函数关系.由于时针、分针在单位时间内转动的角度不变,因此既可以直接写出y1、y2关于x的函数关系式,也可以画出它们的图象.小明选择了后者,画出了图2;
③根据题目的要求,利用函数求解.本题中小明认为求出两个图象交点的横坐标就可以解决问题.
请你按照小明的思路解决这个问题.

(2)请运用建立函数关系的方法解决问题:钟面上,如果把时针与分针看作是同一平面内的两条线段,在7:30~8:00之间,时针与分针互相垂直的时刻是多少? 查看习题详情和答案>>