题目内容
(如图1),点P将线段AB分成一条较小线段AP和一条较大线段BP,如果| AP |
| BP |
| BP |
| AB |
| AP |
| BP |
| BP |
| AB |
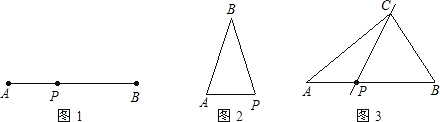
(1)以图1中的AP为底,BP为腰得到等腰△APB(如图2),等腰△APB即为黄金三角形,黄金三角形的定义为:满足
| 底 |
| 腰 |
| 腰 |
| 底+腰 |
(2)如图1,设AB=1,请你说明为什么k约为0.618;
(3)由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果
| S1 |
| S2 |
| S2 |
| S |
(4)图3中的△ABC的黄金分割线有几条?
分析:(1)类比黄金三角形的定义进行定义;
(2)(3)根据线段黄金分割点的概念和三角形的面积公式进行分析;
(4)根据(2)中的结论,得到这样的直线有无数条.
(2)(3)根据线段黄金分割点的概念和三角形的面积公式进行分析;
(4)根据(2)中的结论,得到这样的直线有无数条.
解答:解:
(1)满足
=
≈0.618的矩形是黄金矩形;
(2)由
=k得,BP=1×k=k,从而AP=1-k,
由
=
得,BP2=AP×AB,
即k2=(1-k)×1,
解得k=
,
∵k>0,
∴k=
≈0.618;
(3)因为点P是线段AB的黄金分割点,所以
=
,
设△ABC的AB上的高为h,则
=
=
,
=
=
∴
=
∴直线CP是△ABC的黄金分割线.
(4)由(2)知,在BC边上也存在这样的黄金分割点Q,则AQ也是黄金分割线,设AQ与CP交于点W,则过点W的直线均是△ABC的黄金分割线,故黄金分割线有无数条.
(1)满足
| 宽 |
| 长 |
| 长 |
| 宽+长 |
(2)由
| BP |
| AB |
由
| AP |
| BP |
| BP |
| AB |
即k2=(1-k)×1,
解得k=
-1±
| ||
| 2 |
∵k>0,
∴k=
| ||
| 2 |
(3)因为点P是线段AB的黄金分割点,所以
| AP |
| BP |
| BP |
| AB |
设△ABC的AB上的高为h,则
| S△APC |
| S△BPC |
| ||
|
| AP |
| BP |
| S△BPC |
| S△ABC |
| ||
|
| BP |
| AB |
∴
| S△APC |
| S△BPC |
| S△BPC |
| S△ABC |
∴直线CP是△ABC的黄金分割线.
(4)由(2)知,在BC边上也存在这样的黄金分割点Q,则AQ也是黄金分割线,设AQ与CP交于点W,则过点W的直线均是△ABC的黄金分割线,故黄金分割线有无数条.
点评:注意线段的黄金分割点的概念的延伸,能够根据黄金分割的定义结合三角形的面积进行分析证明.

练习册系列答案
相关题目
 8、如图,已知点D是△ABC中BC边上的一点,线段AD将△ABC分为面积相等的两部分,则线段AD是△ABC的一条( )
8、如图,已知点D是△ABC中BC边上的一点,线段AD将△ABC分为面积相等的两部分,则线段AD是△ABC的一条( )
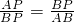 ,那么称点P为线段AB的黄金分割点,设
,那么称点P为线段AB的黄金分割点,设
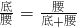 ≈0.618的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义:______;
≈0.618的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义:______; ,那么称直线l为该图形的黄金分割线.(如图3),点P是线段AB的黄金分割点,那么直线CP是△ABC的黄金分割线吗?请说明理由;
,那么称直线l为该图形的黄金分割线.(如图3),点P是线段AB的黄金分割点,那么直线CP是△ABC的黄金分割线吗?请说明理由; ,那么称点P为线段AB的黄金分割点,设
,那么称点P为线段AB的黄金分割点,设 =k,则k就是黄金比,并且k≈0.618.
=k,则k就是黄金比,并且k≈0.618.
 ≈0.618的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义:______;
≈0.618的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义:______; ,那么称直线l为该图形的黄金分割线.(如图3),点P是线段AB的黄金分割点,那么直线CP是△ABC的黄金分割线吗?请说明理由;
,那么称直线l为该图形的黄金分割线.(如图3),点P是线段AB的黄金分割点,那么直线CP是△ABC的黄金分割线吗?请说明理由;