Question

（1）解不等式：

x-3

2

-1＞

x-5

3

（2）做一做：

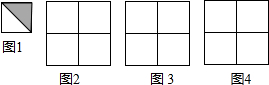
用四块如图1的瓷砖拼成一个正方形，使拼成的图案成轴对称图形，请你在图2，图3，图4中各画出一种拼法（要求三种拼法各不相同，所画图案中的阴影部分用斜线表示）
（3）读一读：
式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和．
由于上述式子比较长，书写也不方便，为了简便起见，我们可以将
“1+2+3+4+5+…+100”表示为

100

n=1

n，这里“Σ”是求和符号．
例如：“1+3+5+7+9+…+99”（即从1开始的100以内的连续奇数的和）可表示为

50

n=1

(2n-1)；又如：“1³+2³+3³+4³+5³+6³+7³+8³+9³+10³”可表示为

10

n=1

n3．
同学们，通过对以上材料的阅读，请解答下列问题：
＜1＞2+4+6+8+10+…+100（即从2开始的100以内的连续偶数的和）用求和符号可表示为

 

；
＜2＞计算：

5

n=1

(n2-1)=

 

（填写最后的计算结果）．

Answer 1

分析：（1）根据分式不等式的解法；先通分，再移项，最后化简可得其解集；
（2）根据轴对称的定义，结合题意；可得答案，注意全面考虑多种情况；
（3）根据题意的表述，可得“Σ”这个求和符号的意义与表示方法，进而可2+4+6+8+10+…+100的表示方法，最后得到

5

n=1

(n2-1)=1+3+8+15+24，计算可得答案．

解答：解：（1）3（x-3）-6＞2（x-5），（2分）
3x-9-6＞2x-10，（3分）
3x-2x＞-10+9+6，（4分）
x＞5．（5分）
（2）

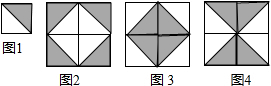
（1分），共（3分）．

（3）①

50

n=1

2n．（1分）
②∑limit

s

5 n=1

(n2-1)=0+3+8+15+24=50．（1分）

点评：本题是一道找规律的题目，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．