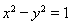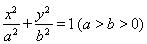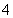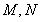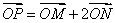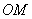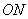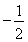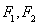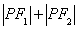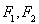网址:http://m.1010jiajiao.com/timu_id_13163[举报]
一、选择题 1-5 D D A C B 6-10 C B D A D 11 A 12 D
二、填空题13.丙 14. 15.
15.  16.
16.
三、解答题
17(1)解:∵p与q是共线向量
∴(2-2sin A)(1+sin A)-(cos A+sin A)(sin A-cos A)=0 2分
整理得: ,∴
,∴ 4分
4分
∵△ABC为锐角三角形,∴A=60° 6分
(2) 
 10分
10分
当B=60°时取函数取最大值2.
此时三角形三内角均为60° 12分
18. 解:(1)由已知,甲队5名队员连续有3人射中,另外2人未射中的概率为
 ……………………6分
……………………6分
(2)两队各射完5个点球后甲胜出,比分为3:1的概率为
 …………………………12分
…………………………12分
 19.本小题满分12分)
19.本小题满分12分)
解:(I)在直三棱柱ABC― 中,AA1⊥面ABC
中,AA1⊥面ABC
∴AA1⊥BC
又∵∠ABC=90°
∴BC⊥面ABB1A1
又 面ABB1A1
面ABB1A1
∴BC⊥A1E 3分
(II)连接AC1交A1C于点F,则F为AC1的中点

又∵E为AB的中点 ∴EF∥BC1 5分
又EF 面A1CE ∴BC1∥面A1CE 6分
面A1CE ∴BC1∥面A1CE 6分
(III)∵面ACA1⊥面ABC,作EO⊥AC,则EO⊥面ACA1,
作OG⊥A1C,则∠OGE为二面角A―A1C―E的平面角 8分
又∵直线A1C与面ABC成45°角
∴∠A1CA=45°
又 ,E为AB的中点 ∴
,E为AB的中点 ∴
∴ 11分
11分
∴
∴二面角A―A1C―E的正切值为 12分
12分
20.解: ,
,
(1)
 是的
是的 极小值点,
极小值点,

 .
.
(2)令
 ……. ①
……. ①
当 时,
时,
当 时,
时,
 ….②
….②
① - ② 得:




21解: …………………2分
…………………2分
①
当 即
即 时,
时,


 (舍)
…………………5分
(舍)
…………………5分
②
当 即
即 时
时


 又
又
∴  …………………8分
…………………8分
③
当 即
即 时
时


 又
又
∴ ………………11分
………………11分
综上所述 ………………12
………………12
22.解:(Ⅰ)设所求双曲线的方程为
抛物线 的焦点F
的焦点F ∴
∴ ,即
,即
又双曲线过点 ∴
∴ ,解得
,解得
故所求双曲线的方程为
(Ⅱ) 直线 .消去方程组
.消去方程组 中的
中的 并整理,得
并整理,得 . ①
. ①
设 ,由已知有
,由已知有 ,且
,且 是方程①的两个实根,
是方程①的两个实根,
∴ ,
, ,
,  .
.
(Ⅲ)  解之,得
解之,得 或
或 .
.
∵ ,∴
,∴ ,
, , 因此,
, 因此, .
.
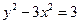 的上支上一点
的上支上一点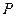 作双曲线的切线交两条渐近线分别于点
作双曲线的切线交两条渐近线分别于点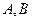 .
.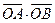 为定值;
为定值;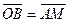 ,求动点
,求动点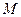 的轨迹方程.
的轨迹方程.