网址:http://m.1010jiajiao.com/timu_id_11979[举报]
一、选择题
BCDC BBCB AA
二、填空题
11.(-1,0);12.4;13.-4;14.-1;15.;16.x2(注:本题答案不唯一,只要满足条件 a¹0,2|a|+|b|≤1即可)
三、解答题
17.解:由条件知20cos
解得sin
(1) 若∠C=60º,则cos2B=cos2(120º-A)=cos(240º
=-. ??????????????????????????????????????????????????????????????7分
(2) 若a<b<c,则A<60º.又由sin
∵(sinA-cosA)2=1-sin
18.解:(1)设P(x,y),则 =(x+1,y),
=(x+1,y), =(x-1,y),
=(x-1,y),
∵ ,∴(x+1)2=(x-1)2+y2,????????????????????????????????????????????????????????????????????????2分
,∴(x+1)2=(x-1)2+y2,????????????????????????????????????????????????????????????????????????2分
即y2=4x.
动点P的轨迹E的方程是y2=4x. ???????????????????????????????????????????????????????????????????????4分
(2)设直线l的方程为x=k(y-1),代入轨迹E的方程y2=4x,整理得:y2-4ky+4k=0. ?????????6分
由题意知,(4k)2-4´4k>0且4k>0,解得k>1. ???????????????????????????????????????????????????????????8分
由根与系数的关系可得MN的中点坐标为(k(2k-1),2k),
∴线段MN垂直平分线方程为:y-2k=-k[x-k(2k-1)], ?????????????????????????????????10分
令y=0,得D点的横坐标x0=2k2-k+2,
∵k>1,∴x0>3,即为所求. ??????????????????????????????????????????????????????????????????????????????????14分
19.(1)证明:连结C1E,则C1E^A1B1,
又∵A1B
而A1B1//AB,∴AB^DE. ????????????????????????????????????????????????????????????????????????????????????????????4分
(2)取AB中点为F,连结EF,DF,则EF^AB,∴AB^DF.
过E作直线EH^DF于H点,则EH^平面DAB,∴EH就是直线A1B1到平面DAB的距离.
在矩形C1EFC中,∵AA1=AB=2,∴EF=2,C1E=,DF=2,
∴在△DEF中,EH=,
故直线A1B1到平面DAB的距离为. ???????????????????????????????????????????????????????????9分
(3)过A作AM^BC于M点,则AM^平面CDB,
过M作MN^BD于N点,连结AN,则AN^BD,∴∠ANM即为所求二面角的平面角,
在Rt△DCB中,BC=2,DC=1,M为BC中点,∴MN=,
在Rt△AMN中,tan∠ANM=,
故二面角A-BD-C的大小为arctan. ???????????????????????????????????????????????????????????????14分
20.解:(1)设从明年开始经过第n年,方案乙的累计总收益为正数。
在方案乙中,前4年的总收入为
=2600<6000, ?????????????????????????????????????????1分
故n必定不小于5,则由
2600+320´1.54(n-4)>6000, ?????????????????????????????????????4分
解得 n>6,故n的最小值为7,
答: 从明年开始至少经过7年,方案乙能收回投资。 ????????????????????????????????????????????6分
(2)设从明年开始经过n年方案甲与方案乙的累计总收益分别为y1,y2万元,则
y1=760n-[50n+n(n-1)?20]=-10n2+720n, ???????????????????????????????????????????????????????????????8分
当n≤4时,则y1>0,y2<0,可得y1>y2. ???????????????????????????????????????????????????????????9分
当n³5时,y2=2600+320´1.54(n-4)-6000=1620n-9880,
令y1<y2,可得1620n-9880>-10n2+720n,
即 n(n+90)>998, ??????????????????????????????????????????????????????????????????????????????????????????????????12分
由10(10+90)>998,9(9+90)<998,可得n的最小值为10.
答:从明年开始至少经过10年,方案乙的累计总收益超过方案甲。 ??????????????????14分
21.解: (1)设0≤x1<x2≤1,则必存在实数tÎ(0,1),使得x2=x1+t,
由条件③得,f(x2)=f(x1+t)³f(x1)+f(t)-2,
∴f(x2)-f(x1)³f(t)-2,
由条件②得, f(x2)-f(x1)³0,
故当0≤x≤1时,有f(0)≤f(x)≤f(1). ????????????????????????????????????????????????????????????3分
又在条件③中,令x1=0,x2=1,得f(1)³f(1)+f(0)-2,即f(0)≤2,∴f(0)=2, ??????????????????????????????5分
故函数f(x)的最大值为3,最小值为2. ???????????????????????????????????6分
(2)解:在条件③中,令x1=x2=,得f()³
故当nÎN*时,有f()-2≤[f()-2]≤[f()-2]≤???≤[f()-2]=,
即f()≤+2.
又f()=f(1)=3≤2+,
所以对一切nÎN,都有f()≤+2. ???????????????????????????????????????????????12分
(3)对一切xÎ(0,1 ,都有
,都有 .
.
对任意满足xÎ(0,1 ,总存在n(nÎN),使得
,总存在n(nÎN),使得
<x≤, ????????????????????????????????????????????????????????????????????????14分
根据(1)(2)结论,可知:
f(x)≤f()≤+2,
且2x+2>2´+2=+2,
故有 .
.
综上所述,对任意xÎ(0,1 ,
, 恒成立.
?????????????????????????????????????????????16分
恒成立.
?????????????????????????????????????????????16分
(13分,理科做)已知函数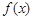 的定义域为
的定义域为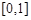 ,且同时满足:①
,且同时满足:①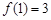 ;②
;②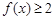 恒成立;③若
恒成立;③若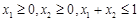 ,则有
,则有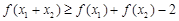 .
.
(1)试求函数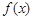 的最大值和最小值;
的最大值和最小值;
(2)试比较 与
与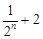 的大小
的大小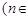 N);
N);
(3)某人发现:当x= (nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1
(nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1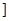 ,都有
,都有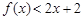 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.
查看习题详情和答案>>