题目内容
(13分,理科做)已知函数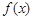 的定义域为
的定义域为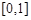 ,且同时满足:①
,且同时满足:①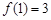 ;②
;②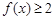 恒成立;③若
恒成立;③若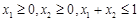 ,则有
,则有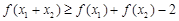 .
.
(1)试求函数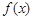 的最大值和最小值;
的最大值和最小值;
(2)试比较 与
与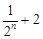 的大小
的大小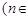 N);
N);
(3)某人发现:当x= (nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1
(nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1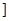 ,都有
,都有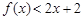 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.
【答案】
(理)解: (1)设0≤x1<x2≤1,则必存在实数tÎ(0,1),使得x2=x1+t,
由条件③得,f(x2)=f(x1+t)³f(x1)+f(t)-2,
∴f(x2)-f(x1)³f(t)-2,
由条件②得, f(x2)-f(x1)³0,
故当0≤x≤1时,有f(0)≤f(x)≤f(1).
又在条件③中,令x1=0,x2=1,得f(1)³f(1)+f(0)-2,即f(0)≤2,∴f(0)=2,
故函数f(x)的最大值为3,最小值为2.
(2)解:在条件③中,令x1=x2=,得f()³2f()-2,即f()-2≤[f()-2],
故当nÎN*时,有f()-2≤[f()-2]≤[f()-2]≤···≤[f()-2]=,
即f()≤+2.
又f()=f(1)=3≤2+,所以对一切nÎN,都有f()≤+2.
(3)对一切xÎ(0,1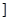 ,都有
,都有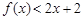 .对任意满足xÎ(0,1
.对任意满足xÎ(0,1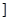 ,总存在n(nÎN),使得
,总存在n(nÎN),使得
<x≤, 根据(1)(2)结论,可知:f(x)≤f()≤+2,
且2x+2>2´+2=+2,故有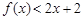 .
.
综上所述,对任意xÎ(0,1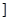 ,
,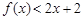 恒成立.
恒成立.
【解析】略

练习册系列答案
相关题目
 (Ⅱ)求二面角M-BC'-B'的大小;
(Ⅱ)求二面角M-BC'-B'的大小;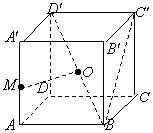 (Ⅱ)求二面角M-BC'-B'的大小;
(Ⅱ)求二面角M-BC'-B'的大小;