摘要：19．证明:(1)面A1B1C1∥面ABC 故B1C1∥BC.A1C1∥AC又BC⊥AC 则B1C1⊥A1C1又 面AB1C⊥面ABC 则BC⊥面AB1C 则BC⊥AB1B1C1⊥AB1 又∵B1C1∩A1C1=C1 B1C1∩AB1=B1故B1C1为异面直线AB1与A1C1的公垂线-----....4分(2)由于BC⊥面AB1C 则面VBC⊥面AB1C过A作AH⊥B1C于H.则AH⊥面VBC

网址：http://m.1010jiajiao.com/timu_id_117690[举报]

（2012•青岛二模）如图，在多面体ABC-A1B1C1中，四边形ABB1A1是正方形，AC=AB=1，A1C=A1B，B1C1∥BC，B1C1=
12
BC．
（Ⅰ）求证：面A1AC⊥面ABC；
（Ⅱ）求证：AB1∥面A1C1C．
 查看习题详情和答案>>
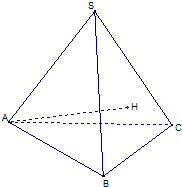已知三棱锥S-ABC的底面是正三角形，A点在侧面SBC上的射影H是△SBC的垂心．
（1）求证：BC⊥SA
（2）若S在底面ABC内的射影为O，证明：O为底面△ABC的中心；
（3）若二面角H-AB-C的平面角等于30°，SA=2
3
，求三棱锥S-ABC的体积．
 查看习题详情和答案>>
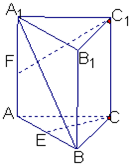已知直棱柱ABC-A1B1C1中，底面△ABC为等腰直角三角形，AC=BC=2
2
，∠ACB=90°，AA1=4，E是AB的中点，F是AA1的中点，
（1）求证A1B⊥CE；
（2）求C1F与侧面ABB1A1所成角的正切值；
（3）求异面直线A1B与C1F所成角．
 查看习题详情和答案>>
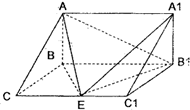精英家教网如图，直三棱柱ABC-A1B1C1中，AB⊥BC，E为棱CC1的中点，已知AB=
2
，BB1=2，BC=1．
（1）证明：BE是异面直线AB与EB1的公垂线；
（2）求二面角A-EB1-A1的大小；
（3）求点A1到面AEB1的距离． 查看习题详情和答案>>
如图所示的集合体是将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右水平平移后得到的．A，A′，B，B′分别为
CD
，
C′D′
，
DE
，
D′E′
的中点，O1，
O
′
1
，O2，
O
′
2
分别为CD，C′D′，DE，D′E′的中点．
（1）证明：
O
′
1
，A′，O2，B四点共面；
（2）设G为A A′中点，延长A′
O
′
1
到H′，使得
O
′
1
H′=A′
O
′
1
．证明：B
O
′
2
⊥平面H′B′G′．
 查看习题详情和答案>>

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网