题目内容
 (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=| 1 | 2 |
(Ⅰ)求证:面A1AC⊥面ABC;
(Ⅱ)求证:AB1∥面A1C1C.
分析:(Ⅰ)利用线面垂直,证明面面垂直,先证明A1A⊥面ABC,再证明面A1AC⊥面ABC;
(Ⅱ)取BC的中点E,证明四边形CEB1C1为平行四边形,可得B1E∥C1C,从而可得B1E∥面A1C1C,再证明AE∥面A1C1C,利用面面平行的判定,可得面B1AE∥面A1C1C,从而可得AB1∥面A1C1C.
(Ⅱ)取BC的中点E,证明四边形CEB1C1为平行四边形,可得B1E∥C1C,从而可得B1E∥面A1C1C,再证明AE∥面A1C1C,利用面面平行的判定,可得面B1AE∥面A1C1C,从而可得AB1∥面A1C1C.
解答: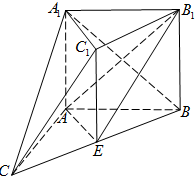 证明:(Ⅰ)∵四边形ABB1A1为正方形,∴A1A=AB=AC=1,A1A⊥AB
证明:(Ⅰ)∵四边形ABB1A1为正方形,∴A1A=AB=AC=1,A1A⊥AB
∴A1B=
…(2分)
∵A1C=A1B,∴A1C=
,∴∠A1AC=90°
∴A1A⊥AC…(4分)
∵AB∩AC=A,∴A1A⊥面ABC
又∵A1A?面A1AC,∴面A1AC⊥面ABC…(6分)
(Ⅱ)取BC的中点E,连接AE,C1E,B1E
∵B1C1∥BC,B1C1=
BC,∴B1C1∥EC,B1C1=EC
∴四边形CEB1C1为平行四边形,∴B1E∥C1C
∵C1C?面A1C1C,B1E?面A1C1C,∴B1E∥面A1C1C…(8分)
∵B1C1∥BC,B1C1=
BC,∴B1C1∥BE,B1C1=BE
∴四边形BB1C1E为平行四边形,∴B1B∥C1E,且B1B=C1E
又∵ABB1A1是正方形,∴A1A∥C1E,且A1A=C1E
∴AEC1A1为平行四边形,∴AE∥A1C1,
∵A1C1?面A1C1C,AE?面A1C1C,∴AE∥面A1C1C…(10分)
∵AE∩B1E=E,∴面B1AE∥面A1C1C
∵AB1?面B1AE,∴AB1∥面A1C1C…(12分)
 证明:(Ⅰ)∵四边形ABB1A1为正方形,∴A1A=AB=AC=1,A1A⊥AB
证明:(Ⅰ)∵四边形ABB1A1为正方形,∴A1A=AB=AC=1,A1A⊥AB∴A1B=
| 2 |
∵A1C=A1B,∴A1C=
| 2 |
∴A1A⊥AC…(4分)
∵AB∩AC=A,∴A1A⊥面ABC
又∵A1A?面A1AC,∴面A1AC⊥面ABC…(6分)
(Ⅱ)取BC的中点E,连接AE,C1E,B1E
∵B1C1∥BC,B1C1=
| 1 |
| 2 |
∴四边形CEB1C1为平行四边形,∴B1E∥C1C
∵C1C?面A1C1C,B1E?面A1C1C,∴B1E∥面A1C1C…(8分)
∵B1C1∥BC,B1C1=
| 1 |
| 2 |
∴四边形BB1C1E为平行四边形,∴B1B∥C1E,且B1B=C1E
又∵ABB1A1是正方形,∴A1A∥C1E,且A1A=C1E
∴AEC1A1为平行四边形,∴AE∥A1C1,
∵A1C1?面A1C1C,AE?面A1C1C,∴AE∥面A1C1C…(10分)
∵AE∩B1E=E,∴面B1AE∥面A1C1C
∵AB1?面B1AE,∴AB1∥面A1C1C…(12分)
点评:本题考查面面垂直,考查线面平行,解题的关键是掌握面面垂直的判定方法,正确运用面面平行判断线面平行,属于中档题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 (2012•青岛二模)已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图示.
(2012•青岛二模)已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图示.