题目内容
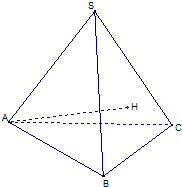 已知三棱锥S-ABC的底面是正三角形,A点在侧面SBC上的射影H是△SBC的垂心.
已知三棱锥S-ABC的底面是正三角形,A点在侧面SBC上的射影H是△SBC的垂心.(1)求证:BC⊥SA
(2)若S在底面ABC内的射影为O,证明:O为底面△ABC的中心;
(3)若二面角H-AB-C的平面角等于30°,SA=2
| 3 |
分析:(1)由AH⊥面SBC,BC在面SBC内,知H是△SBC的垂心,故SH⊥BC,由此能够证明BC⊥SA.
(2)由SO⊥面ABC,知SO⊥BC,由BC⊥SA,知BC⊥面SOA,故AO⊥BC,同理AB⊥OC,由此能够证明故O为底面△ABC的中心.
(3)由(1)有SA=SB=SC=2
,设CO交AB于F,则CF⊥AB,CF是EF在面ABC内的射影,得到∠EFC为二面角H-AB-C的平面角,由此能求出三棱锥S-ABC的体积.
(2)由SO⊥面ABC,知SO⊥BC,由BC⊥SA,知BC⊥面SOA,故AO⊥BC,同理AB⊥OC,由此能够证明故O为底面△ABC的中心.
(3)由(1)有SA=SB=SC=2
| 3 |
解答: 证明:(1)∵AH⊥面SBC,BC在面SBC内,
证明:(1)∵AH⊥面SBC,BC在面SBC内,
∴AH⊥BC,
∵H是△SBC的垂心,∴SH⊥BC,
又∵SH∩AH=H,∴BC⊥面SAH,
∴BC⊥SA.…(4分)
又∵BC⊥SA,SA∩SO=S,
∴BC⊥面SOA,
∴AO⊥BC,同理AB⊥OC,…(8分)
因此O为底面△ABC的垂心,
而三棱锥S-ABC的底面是正三角形,
故O为底面△ABC的中心.
(3)由(1)有SA=SB=SC=2
,
设CO交AB于F,则CF⊥AB,CF是EF在面ABC内的射影,
∴EF⊥AB,∴∠EFC为二面角H-AB-C的平面角,
∠EFC=30°,∠ECF=60°,
OC=
,SO=3,AB=3,
S△ABC=
•32=
,
∴VS-ABC=
S△ABC•SO=
.…(14分)
 证明:(1)∵AH⊥面SBC,BC在面SBC内,
证明:(1)∵AH⊥面SBC,BC在面SBC内,∴AH⊥BC,
∵H是△SBC的垂心,∴SH⊥BC,
又∵SH∩AH=H,∴BC⊥面SAH,
∴BC⊥SA.…(4分)
|
又∵BC⊥SA,SA∩SO=S,
∴BC⊥面SOA,
∴AO⊥BC,同理AB⊥OC,…(8分)
因此O为底面△ABC的垂心,
而三棱锥S-ABC的底面是正三角形,
故O为底面△ABC的中心.
(3)由(1)有SA=SB=SC=2
| 3 |
设CO交AB于F,则CF⊥AB,CF是EF在面ABC内的射影,
∴EF⊥AB,∴∠EFC为二面角H-AB-C的平面角,
∠EFC=30°,∠ECF=60°,
OC=
| 3 |
S△ABC=
| ||
| 4 |
9
| ||
| 4 |
∴VS-ABC=
| 1 |
| 3 |
9
| ||
| 9 |
点评:本题考查异面直线垂直的证明,考查三角形中心的证明,考查三棱锥体积的求法,解题时要认真审题,仔细解答,合理地化空间问题为平面问题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目