题目内容
 如图所示的集合体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右水平平移后得到的.A,A′,B,B′分别为
如图所示的集合体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右水平平移后得到的.A,A′,B,B′分别为 |
| CD |
 |
| C′D′ |
 |
| DE |
 |
| D′E′ |
| O | ′ 1 |
| O | ′ 2 |
(1)证明:
| O | ′ 1 |
(2)设G为A A′中点,延长A′
| O | ′ 1 |
| O | ′ 1 |
| O | ′ 1 |
| O | ′ 2 |
分析:(1)利用共面的判断条件证明直线平行即可.
(2)利用线面垂直的判定定理进行判断.
(2)利用线面垂直的判定定理进行判断.
解答: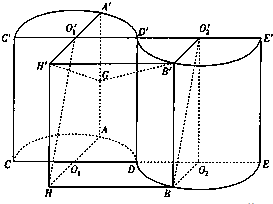 证明:(1)∵A,A′分别为
证明:(1)∵A,A′分别为
,
中点,∴O1′A′∥O1A
连接BO2∵直线BO2是由直线AO1平移得到
∴AO1∥BO2∴O1′A′∥BO2
∴O1′,A′,O2,B共面.
(2)将AO1延长至H使得O1H=O1A,连接HO1′,HB,H′H
∴由平移性质得O1′O2′=HB
∴BO2′∥HO1′,
∵A′G=H′O1′,H′H=A′H′,∠O1′H′H=∠GA′H′=
∴△GA′H′≌△O1′H′H,
∴∠H′O1′H+GH′A=
,
∴O1′H⊥H′G,
∴BO2′⊥H′G.
∵O1′O2′⊥B′O2′,O1′O2′⊥O2′O2,B′O2′∩O2′O2=O2′
∴O1′O2′⊥平面B′BO2O2′
∴O1′O2′⊥BO2′
∴BO2′⊥H′B′,
∵H'B'∩H'G=H'
∴BO2′⊥平面H′B′G.
 证明:(1)∵A,A′分别为
证明:(1)∵A,A′分别为 |
| CD |
 |
| C′D′ |
连接BO2∵直线BO2是由直线AO1平移得到
∴AO1∥BO2∴O1′A′∥BO2
∴O1′,A′,O2,B共面.
(2)将AO1延长至H使得O1H=O1A,连接HO1′,HB,H′H
∴由平移性质得O1′O2′=HB
∴BO2′∥HO1′,
∵A′G=H′O1′,H′H=A′H′,∠O1′H′H=∠GA′H′=
| π |
| 2 |
∴△GA′H′≌△O1′H′H,
∴∠H′O1′H+GH′A=
| π |
| 2 |
∴O1′H⊥H′G,
∴BO2′⊥H′G.
∵O1′O2′⊥B′O2′,O1′O2′⊥O2′O2,B′O2′∩O2′O2=O2′
∴O1′O2′⊥平面B′BO2O2′
∴O1′O2′⊥BO2′
∴BO2′⊥H′B′,
∵H'B'∩H'G=H'
∴BO2′⊥平面H′B′G.
点评:本题主要考查线面垂直的判定定理,综合性较强.

练习册系列答案
相关题目


 如图所示的集合体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右水平平移后得到的.A,A′,B,B′分别为
如图所示的集合体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右水平平移后得到的.A,A′,B,B′分别为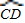 ,
, ,
, ,
,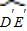 的中点,
的中点,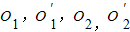 分别为CD,C′D′,DE,D′E′的中点.
分别为CD,C′D′,DE,D′E′的中点.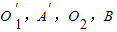 四点共面;
四点共面;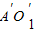 到H′,使得
到H′,使得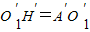 .证明:
.证明: .
.