摘要：(1)在光滑水平面上做加速度大小为g的匀加速直线运动, (2)在光滑斜面上沿斜面向上的匀速直线运动, (3)做竖直向下的匀速直线运动, (4)做竖直向上的加速度大小为g的匀加速直线运动. 设四根弹簧伸长量分别为△l1.△l2.△l3.△l4.不计空气阻力.g为重力加速度.则 A．△l1>△l2 B．△l3<△l4 C．△l1>△l4 D．△l2>△l3
网址：http://m.1010jiajiao.com/timu_id_1090739[举报]
如图所示，在光滑水平面上有一辆长为L、质量为m的绝缘木板小车正以向右的初速度v1=| gL |
（1）求物块与小车上表面间的滑动摩擦因数μ；
（2）若车的初速度为2v0，在物块刚放上小车的同时在空间加一水平向右的匀强电场E1，为了让物块不从车的左端掉下来，求电场强度E1的最小值；
（3）若车的初速度为2v0，在物块刚放上小车的同时在空间加匀强电场E2，其方向在竖直平面内与水平方向夹角为θ=37°斜向右下方．为了让物块始终不从小车上掉下来，求电场强度E2的大小范围．（重力加速度记为g，sin 37°=0.6，cos 37°=0.8）
如图所示.光滑水平面上有一质量M=1.0kg 的小车，小车右端有一个质量m=0.90 kg 的滑块，滑块与小车左端的挡板之间用轻弹簧相连接，滑块与车面间的动摩察因数μ＝0.20，车和滑块一起以v1=10m ／s的速度向右做匀速直线运动，此时弹簧为原长.一质量m0=0.10 kg 的子弹，以v0=50m ／s的速度水平向左射入滑块而没有穿出，子弹射入滑块的时间极短.当弹簧压缩到最短时，弹簧被锁定(弹簧在弹性限度内)，测得此时弹簧的压缩量d=0.50m ，重力加速度g＝10 m／s2，求：
(1)子弹与滑块刚好相对静止的瞬间，子弹与滑块共同速度的大小和方向；
(2)弹簧压缩到最短时，小车的速度大小和弹簧的弹性势能；
(3)如果当弹簧压缩到最短时，不锁定弹簧，则弹簧再次回到原长时，车的速度大小.
如图所示，在光滑水平面上有一辆长为L、质量为m的绝缘木板小车正以向右的初速度
做匀速直线运动．现无初速地释放一个质量也为m，带电量为+q（q > 0）的小物块在小车的正中央，发现物块恰好没有从车上掉下来．
（1）求物块与小车上表面间的滑动摩擦因数μ；
（2）若车的初速度为2v0，在物块刚放上小车的同时在空间加一水平向右的匀强电场E1，为了让物块不从车的左端掉下来，求电场强度E1的最小值；
（3）若车的初速度为2v0，在物块刚放上小车的同时在空间加匀强电场E2，其方向在竖直平面内与水平方向夹角为θ = 37°斜向右下方．为了让物块始终不从小车上掉下来，求电场强度E2的大小范围．（重力加速度记为g，sin 37° = 0.6，cos 37° = 0.8）
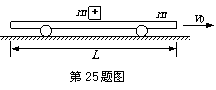
如图所示，在光滑水平面上有一辆长为L、质量为m的绝缘木板小车正以向右的初速度v1=
做匀速直线运动．现无初速地释放一个质量也为m，带电量为+q（q＞0）的小物块在小车的正中央，发现物块恰好没有从车上掉下来．
（1）求物块与小车上表面间的滑动摩擦因数μ；
（2）若车的初速度为2v，在物块刚放上小车的同时在空间加一水平向右的匀强电场E1，为了让物块不从车的左端掉下来，求电场强度E1的最小值；
（3）若车的初速度为2v，在物块刚放上小车的同时在空间加匀强电场E2，其方向在竖直平面内与水平方向夹角为θ=37°斜向右下方．为了让物块始终不从小车上掉下来，求电场强度E2的大小范围．（重力加速度记为g，sin 37°=0.6，cos 37°=0.8）
查看习题详情和答案>>
做匀速直线运动．现无初速地释放一个质量也为m，带电量为+q（q＞0）的小物块在小车的正中央，发现物块恰好没有从车上掉下来．（1）求物块与小车上表面间的滑动摩擦因数μ；
（2）若车的初速度为2v，在物块刚放上小车的同时在空间加一水平向右的匀强电场E1，为了让物块不从车的左端掉下来，求电场强度E1的最小值；
（3）若车的初速度为2v，在物块刚放上小车的同时在空间加匀强电场E2，其方向在竖直平面内与水平方向夹角为θ=37°斜向右下方．为了让物块始终不从小车上掉下来，求电场强度E2的大小范围．（重力加速度记为g，sin 37°=0.6，cos 37°=0.8）
查看习题详情和答案>>
如图所示，光滑水平面上有一质量M=1.0kg的小车，小车右端有一个质量m=0.90kg的滑块，滑块与小车左端的挡板之间用轻弹簧相连接，滑块与车面间的动摩擦因数μ=0.20，车和滑块一起以v1=10m/s的速度向右做匀速直线运动，此时弹簧为原长．一质量m0=0.10kg的子弹，以v0=50m/s的速度水平向左射入滑块而没有穿出，子弹射入滑块的时间极短．当弹簧压缩到最短时，弹簧被锁定（弹簧在弹性限度内），测得此时弹簧的压缩量d=0.50m，重力加速度g=10m/s2，求：（1）子弹与滑块刚好相对静止的瞬间，子弹与滑块共同速度的大小和方向；
（2）弹簧压缩到最短时，小车的速度大小和弹簧的弹性势能；
（3）如果当弹簧压缩到最短时，不锁定弹簧，则弹簧再次回到原长时，车的速度大小．