题目内容
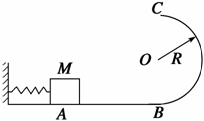
如图所示.光滑水平面上有一质量M=1.(1)子弹与滑块刚好相对静止的瞬间,子弹与滑块共同速度的大小和方向;
(2)弹簧压缩到最短时,小车的速度大小和弹簧的弹性势能;
(3)如果当弹簧压缩到最短时,不锁定弹簧,则弹簧再次回到原长时,车的速度大小.

(1)设子弹和滑块相对静止时共同速度为v,根据动量守恒定律
mv1-m0v0=(m0+m)v
解得:v=4.0m/s
方向向右
(2)设弹簧压缩到最短时它们的共同速度为v′,
根据动量守恒定律Mv1+(m+m0)v=(M+m+m0)v′
解得:v′=7.0m/s
设滑块与车摩擦产生的热为Q,弹簧的最大弹性
势能为Ep,根据能量守恒有:![]() M
M![]() +
+![]() (m+m0)v2=
(m+m0)v2=![]() (M+m+m0)v′2+Q+Ep
(M+m+m0)v′2+Q+Ep
Q=μ(m+m0)gd=1.0J 解得:Ep=8.0J
(3)设弹簧再次回到原长时,车的速度为v1,滑块(和子弹)的速度为v2,根据动量守恒定律(M+m0+m)v′=Mv1+(m0+m)v2
根据能量守恒:![]() (M+m0+m)v′2+Ep=
(M+m0+m)v′2+Ep=![]() M
M![]() +
+![]() (m0+m)
(m0+m)![]() +Q
+Q
解得:车的速度大小为
v1=(7-![]() )m/s=4.
)m/s=4.
(另一解v1=(7+![]() )m/s=9.
)m/s=9.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 如图所示光滑水平面有一长木板其质量为mA=1kg,长木板两端有两小物块.其质量分别为mB=2kg,mc=5kg,已知B与A之间、C与A之间的动摩擦因数均为μ=O.5,现物块C以初速度V.=8m/s向左运动,最终物体C恰好没有与B相碰(g=10m/s2,B、C均可看成质点)
如图所示光滑水平面有一长木板其质量为mA=1kg,长木板两端有两小物块.其质量分别为mB=2kg,mc=5kg,已知B与A之间、C与A之间的动摩擦因数均为μ=O.5,现物块C以初速度V.=8m/s向左运动,最终物体C恰好没有与B相碰(g=10m/s2,B、C均可看成质点)