题目内容
已知两定点A(0,-1),C(0,2),动点M满足∠MCA=2∠MAC.(Ⅰ)求动点M的轨迹Q的方程;
(Ⅱ)设曲线Q与y轴的交点为B,点B、F是曲线Q上两个不同的动点,且![]() =0,直线AE与BF交于点P(x0,y0),求证:
=0,直线AE与BF交于点P(x0,y0),求证:![]() 为定值;
为定值;
(Ⅲ)在第(Ⅱ)问的条件下,求证:过点p′(0,y0)和点E的直线是曲线Q的一条切线.
(Ⅳ)在第(Ⅱ)问的条件下,试问是否存在点E使得![]() (或
(或![]() ),若存在,求出此时点E的坐标;若不存在,说明理由.
),若存在,求出此时点E的坐标;若不存在,说明理由.
解:(Ⅰ)设动点M(x,y),因为∠MCA=2∠MAC
所以
化简得:y2![]() =1(y>1)
=1(y>1)
(Ⅱ)由![]() =0可设点E(x1,y1),F(-x1,y1)则由A、P、E三点共线可得x0(y1+1)=(y0+1)x1,同理可得:x0(y1-1)=-(y0-1)x1,
=0可设点E(x1,y1),F(-x1,y1)则由A、P、E三点共线可得x0(y1+1)=(y0+1)x1,同理可得:x0(y1-1)=-(y0-1)x1,
两式相乘得:![]() (
(![]() -1)=
-1)=![]() (
(![]() -1),又因为
-1),又因为![]() =1,所以=
=1,所以=![]() =3.
=3.
(Ⅲ)点E处曲线Q的切线的斜率为y′=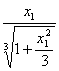 ,则切线方程为x1x-
,则切线方程为x1x-![]() y+3=0,AE、BF的方程为y+1=
y+3=0,AE、BF的方程为y+1=![]() x,y-1=
x,y-1=![]() x,则y0=
x,则y0=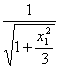 ,
,
所以P′在上述切线上,即过点P′(0,y0)和点E的直线是曲线Q的一条切线.
(Ⅳ)先证:∠CEP′=∠BEA
Tan∠CEP′=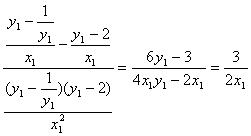 (其中用到
(其中用到![]() 代换)
代换)
Tan∠BEA=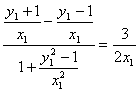 由此可得:∠CEP′=∠BEA.
由此可得:∠CEP′=∠BEA.
要使![]() ,则只需S△CEP′=S△BEA,
,则只需S△CEP′=S△BEA,
即|CP′|=|AB|=2.而|CP′|=2![]() <2,因此不存在点E使得
<2,因此不存在点E使得![]() 成立.
成立.
另解:同前可得∠CEP′=∠BEA,要使
![]() 则只需
则只需![]() ,
,
即![]() +(2-y1)(
+(2-y1)(![]() -y1)=
-y1)=![]() ,化简得-2=0,显然不成立.
,化简得-2=0,显然不成立.

练习册系列答案
相关题目