题目内容
用α、β、γ三个字母组成一个长度为(n+1)(n∈N*)个字母的字符串,要求由α开始,相邻两个字母不同.例如:n=1时,排出的字符串是αβ或αγ;n=2时,排出的字符串是αβα、αβγ、αγα、αγβ(如图).若记这种(n+1)个字符串中,最后一个字母仍是α的字符串的个数为an,可知a1=0,a2=2,a3=2,a4=6,…,则数列{an}的第n项an与第n-1项an-1(n≥2,n∈N*) .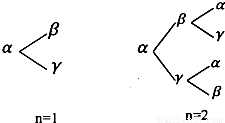
【答案】分析:由a1=0,a2=2,a3=2,a4=6,知a1+a2=2,a2+a3=2+2=4,a3+a4=2+6=8,由此利用合理猜想能够得到an+an-1=2n-1,(n≥2).
解答:解:∵a1=0,a2=2,a3=2,a4=6,
∴a1+a2=2,
a2+a3=2+2=4,
a3+a4=2+6=8,
由此猜想:an+an-1=2n-1,(n≥2).
故答案为:an+an-1=2n-1,(n≥2).
点评:本题考查数列的递推公式的合理运用,是基础题.解题时要认真审题,仔细观察,注意合理猜想.
解答:解:∵a1=0,a2=2,a3=2,a4=6,
∴a1+a2=2,
a2+a3=2+2=4,
a3+a4=2+6=8,
由此猜想:an+an-1=2n-1,(n≥2).
故答案为:an+an-1=2n-1,(n≥2).
点评:本题考查数列的递推公式的合理运用,是基础题.解题时要认真审题,仔细观察,注意合理猜想.

练习册系列答案
相关题目
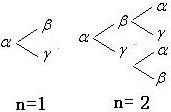 用α,β,γ三个字母组成一个长度为n+1(n∈N*)个字母的字符串,要求由α开始,相邻两个字母不同.例如n=1时,排出的字符串可能是αβ或αγ;n=2时排出的字符串可能是αβα,αβγ,αγα,αγβ(如图).若记这种n+1个字符串中,排在最后一个的字母仍是α的所有字符串的种数为an,可知,a1=0,a2=2;则a4=
用α,β,γ三个字母组成一个长度为n+1(n∈N*)个字母的字符串,要求由α开始,相邻两个字母不同.例如n=1时,排出的字符串可能是αβ或αγ;n=2时排出的字符串可能是αβα,αβγ,αγα,αγβ(如图).若记这种n+1个字符串中,排在最后一个的字母仍是α的所有字符串的种数为an,可知,a1=0,a2=2;则a4=