0 53731 53739 53745 53749 53755 53757 53761 53767 53769 53775 53781 53785 53787 53791 53797 53799 53805 53809 53811 53815 53817 53821 53823 53825 53826 53827 53829 53830 53831 53833 53835 53839 53841 53845 53847 53851 53857 53859 53865 53869 53871 53875 53881 53887 53889 53895 53899 53901 53907 53911 53917 53925 447348
 2或a
2或a 3 B.2
3 B.2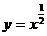 .则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是( )
.则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是( )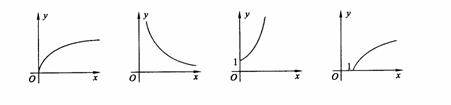 A.②①③④ B.②③①④ C.④①③② D.④③①②
A.②①③④ B.②③①④ C.④①③② D.④③①②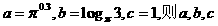 的大小关系是( )
的大小关系是( )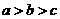 B.
B. 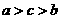 C.
C. 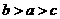 D.
D. 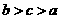
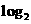 a<0,
a<0,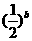 >1,则( )
>1,则( ) 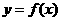 是函数
是函数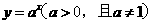 的反函数,且
的反函数,且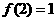 ,则
,则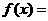 ( )
( )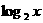 B.
B.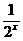 C.
C.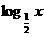 D.2
D.2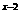
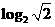 的值为( )
的值为( )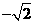 B.
B.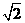 C.
C.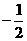 D.
D. 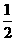
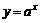 (
(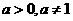 )与
)与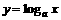 互为反函数.
互为反函数.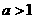 时,
时,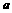 值越大,越靠近
值越大,越靠近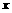 轴;当
轴;当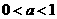 时,则相反.
时,则相反.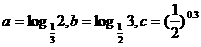 ,则( )
,则( )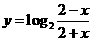 的图像( )
的图像( )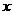 轴对称 (C)关于
轴对称 (C)关于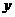 轴对称 (D)关于直线
轴对称 (D)关于直线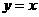 对称
对称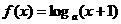 ,
,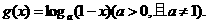 (1)求
(1)求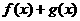 的定义域;(2)判断
的定义域;(2)判断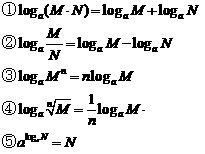
 为实数,函数
为实数,函数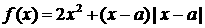 .
. 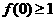 ,求
,求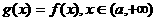 的最小值.
的最小值.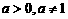 )的
)的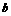 次幂等于
次幂等于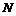 ,
,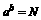 ,数
,数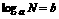 (
(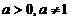 ,负数和零没有对数);
,负数和零没有对数);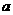 叫底数,
叫底数,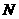 叫真数.
叫真数.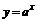 (
(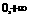 ).
).  ,指数函数:
,指数函数: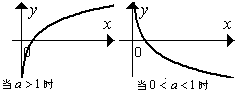 ⑵当
⑵当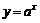 的
的