1.解:(Ⅰ)∵ 定义域为
定义域为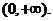
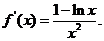 ∵
∵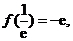 又∵
又∵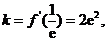
∴函数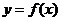 在
在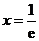 处的切线方程为:
处的切线方程为: 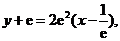 即:
即: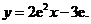
(Ⅱ)令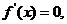 得
得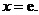 ∵当
∵当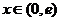 时,
时,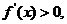
 在
在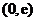 上为增函数;
上为增函数;
当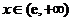 时,
时,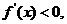
 在
在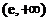 上为减函数; ∴
上为减函数; ∴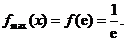
2解:(Ⅰ)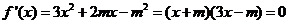 ,则
,则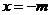 或
或 ,
,
当x变化时, 与
与 的变化情况如下表:
的变化情况如下表:
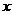 |
(-∞,-m) |
-m |
(-m,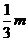 ) ) |
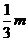 |
(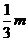 ,+∞) ,+∞) |
 ) ) |
+ |
0 |
- |
0 |
+ |
 |
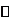 |
极大值 |
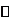 |
极小值 |
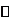 |
从而可知,当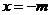 时,函数
时,函数 取得极大值9,即
取得极大值9,即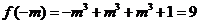
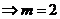 .
.
(Ⅱ)由(Ⅰ)知,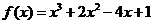 ,依题意知
,依题意知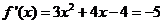 ,∴
,∴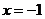 或
或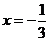
又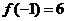 ,
,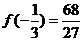 ,所以切线方程为
,所以切线方程为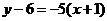 ),或
),或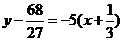 ,
,
即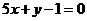 ,或
,或 .
.
3解.(Ⅰ) 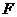

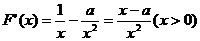
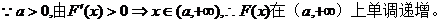
由 。
。
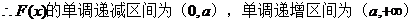
(Ⅱ)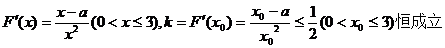
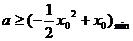 当
当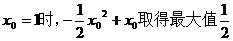
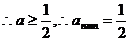 ………………………………………
………………………………………
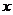 年的年平均污水处理费用
年的年平均污水处理费用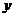 (万元);
(万元);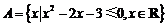 ,
,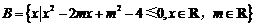 .
.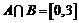 ,求实数
,求实数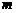 的值;(Ⅱ)若
的值;(Ⅱ)若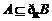 ,求实数
,求实数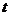 (天)的函数,且销售量近似地满足
(天)的函数,且销售量近似地满足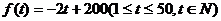 ,前30天价格为
,前30天价格为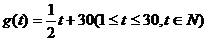 ,后20天价格为
,后20天价格为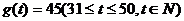 。
。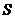 与时间
与时间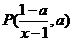 与定点
与定点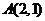 在直线
在直线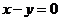 的同侧。
的同侧。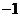 是这个不等式的解,求
是这个不等式的解,求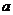 的取值范围。(3)已知
的取值范围。(3)已知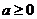 ,求这个关于
,求这个关于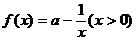
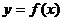 在(0,
在(0,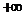 )上是增函数;
)上是增函数;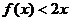 在[1,
在[1,