(19) (本小题满分12分)
设函数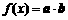 ,其中向量
,其中向量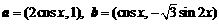 ,
, .
.
(Ⅰ)求函数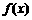 的单调减区间;
的单调减区间;
(Ⅱ)若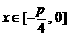 ,求函数
,求函数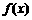 的值域;
的值域;
(Ⅲ)若函数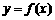 的图象按向量
的图象按向量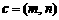
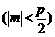 平移后得到函数
平移后得到函数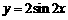 的图象,求实数
的图象,求实数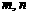 的值.
的值.
(20) (本小题满分12分)
在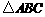 中,
中,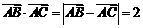 .
.
(Ⅰ)求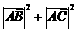 的值;
的值;
(Ⅱ)当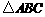 的面积最大时,求
的面积最大时,求 的大小.
的大小.
(21) (本小题满分14分)
设函数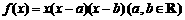 .
.
(Ⅰ)若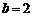 ,证明函数
,证明函数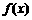 有两个不同的极值点
有两个不同的极值点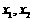 ,并且
,并且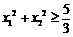 ;
;
(Ⅱ)若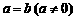 ,且当
,且当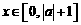 时,
时,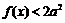 恒成立,求
恒成立,求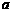 的取值范围.
的取值范围.
(22) (本小题满分14分)
某市电信宽带私人用户月收费标准如下表:
|
方案 |
类 别 |
基本费用 |
超时费用 |
|
甲 |
包月制 |
70元 |
|
|
乙 |
有限包月制(限60小时) |
50元 |
0.05元/分钟(无上限) |
|
丙 |
有限包月制(限30小时) |
30元 |
0.05元/分钟(无上限) |
假定每月初可以和电信部门约定上网方案.
(Ⅰ)若某用户每月上网时间为66小时,应选择 ▲ 方案最合算;
(Ⅱ)王先生因工作需要在家上网,所在公司预测其一年内每月的上网时间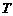 (小时)与月份
(小时)与月份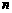 的函数关系为
的函数关系为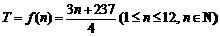 .若公司能报销王先生全年上网费用,问公司最少会为此花费多少元?
.若公司能报销王先生全年上网费用,问公司最少会为此花费多少元?
(Ⅲ)一年后,因公司业务变化,王先生每月的上网时间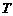 (小时)与月份
(小时)与月份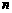 的函数关系为
的函数关系为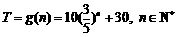 .假设王先生退休前一直从事此项业务,公司在花费尽量少的前提下,除为其报销每月的基本费用外,对于所有的超时费用,公司考虑一次性给予补贴
.假设王先生退休前一直从事此项业务,公司在花费尽量少的前提下,除为其报销每月的基本费用外,对于所有的超时费用,公司考虑一次性给予补贴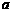 元,试确定最合理的
元,试确定最合理的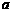 的值,并说明理由.
的值,并说明理由.
(23) (本小题满分14分)
已知函数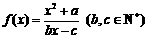 ,并且
,并且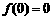 ,
,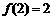 ,
,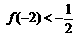 .
.
(Ⅰ)求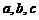 的值;
的值;
(Ⅱ)是否存在各项均不为零的数列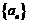 ,满足
,满足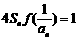 (
(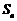 为数列
为数列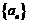 的前
的前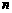 项和).若有,写出数列的一个通项公式
项和).若有,写出数列的一个通项公式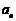 ,并说明满足条件的数列
,并说明满足条件的数列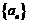 是否唯一确定;若无,请说明理由.
是否唯一确定;若无,请说明理由.
江苏省苏州市部分重点中学2006届高三期中考试试卷
(1)已知平面向量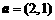 ,
,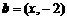 ,且
,且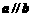 ,则
,则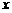 的值为 ( )
的值为 ( )
A.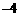 B.
B.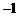 C.1 D.4
C.1 D.4
(2)已知集合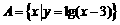 ,
,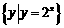 ,则
,则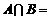 ( )
( )
A.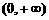 B.
B.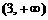 C.
C.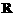 D.
D.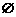
(3)已知函数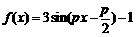 ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )
A.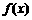 是周期为1的奇函数 B.
是周期为1的奇函数 B.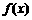 是周期为2的偶函数
是周期为2的偶函数
C.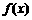 是周期为1的非奇非偶函数 D.
是周期为1的非奇非偶函数 D.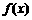 是周期为2的非奇非偶函数
是周期为2的非奇非偶函数
(4)设等差数列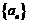 的前
的前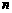 项和为
项和为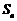 ,若
,若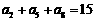 ,则
,则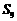 等于 ( )
等于 ( )
A.18 B.36 C.45 D.60
(5)函数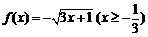 的反函数 ( )
的反函数 ( )
A.在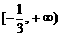 上单调递增 B.在
上单调递增 B.在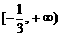 上单调递减
上单调递减
C.在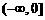 上单调递增 D.在
上单调递增 D.在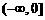 上单调递减
上单调递减
(6)设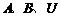 均为非空集合,且满足
均为非空集合,且满足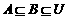 ,则下列各式中错误的是 ( )
,则下列各式中错误的是 ( )
A.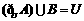 B.
B.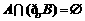
C.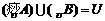 D.
D.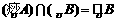
(7)命题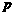 :
: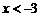 是
是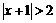 的充分不必要条件;
命题
的充分不必要条件;
命题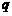 :在
:在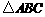 中,如果
中,如果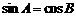 ,那么
,那么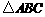 为直角三角形.则 ( )
为直角三角形.则 ( )
A.“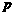 或
或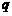 ”为假 B.“
”为假 B.“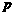 且
且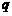 ”为真 C.
”为真 C.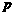 假
假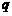 真 D.
真 D.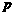 真
真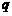 假
假
(8)设函数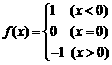 ,则当
,则当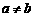 时,
时,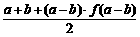 的值应为 ( )
的值应为 ( )
A. B.
B.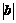 C.
C.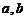 中的较小数 D.
中的较小数 D.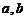 中的较大数
中的较大数
(9)函数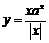
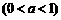 的图象的大致形状是 ( )
的图象的大致形状是 ( )
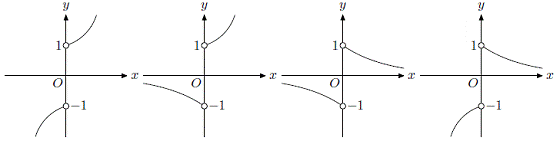
A B C D
(10)在 中,
中, ,则
,则 边上的高为 ( )
边上的高为 ( )
A.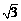 B.
B.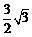 C.1 D.
C.1 D.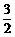
(11)已知函数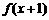 为奇函数,函数
为奇函数,函数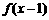 为偶函数,且
为偶函数,且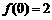 ,则
,则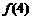 = ( )
= ( )
A.2 B.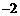 C.4 D.
C.4 D.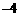
(12)为了稳定市场,确保农民增收,某农产品的市场收购价格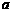 与其前三个月的市场收购价格有关,且使
与其前三个月的市场收购价格有关,且使 与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
|
月份 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
价格(元/担) |
68 |
78 |
67 |
71 |
72 |
70 |
|
则7月份该产品的市场收购价格应为 ( )
A.69元 B.70元 C.71元 D.72元
第Ⅱ卷(非选择题 共90分)
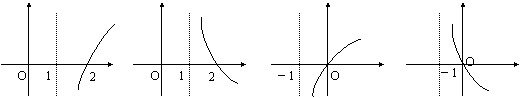
 (18)(本小题满分14分)如图,在多面体ABCDE中,AE⊥面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F为CD的中点.
(18)(本小题满分14分)如图,在多面体ABCDE中,AE⊥面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F为CD的中点. 平面BCD.
平面BCD.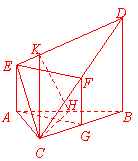 (II)设AB中点为H,则由AC=AB=BC=2,可得CH⊥AB且CH=.
(II)设AB中点为H,则由AC=AB=BC=2,可得CH⊥AB且CH=.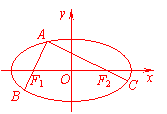 即 |AF1|=,|AF2|=,
即 |AF1|=,|AF2|=, (14)将一张画有直角坐标系的图纸折叠一次,使得点A(0,2)与点B(4,0)重合.若此时点C(7,3)与点D(m,n)重合,则m+n的值是 .
(14)将一张画有直角坐标系的图纸折叠一次,使得点A(0,2)与点B(4,0)重合.若此时点C(7,3)与点D(m,n)重合,则m+n的值是 .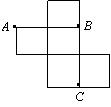 (15)如图,是一个无盖正方体盒子的表面展开图,A,B,C为其上的三个点,则在正方体盒子中,∠ABC等于 60o .
(15)如图,是一个无盖正方体盒子的表面展开图,A,B,C为其上的三个点,则在正方体盒子中,∠ABC等于 60o . α (D)m,n与α所成角相等
α (D)m,n与α所成角相等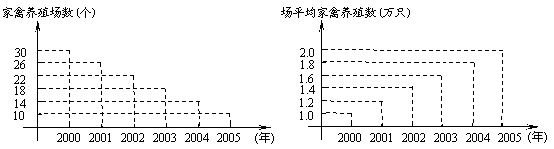
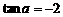 ,则
,则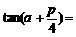 ▲ .
▲ .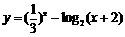 在区间
在区间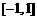 上的最大值为 ▲ .
上的最大值为 ▲ .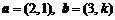 ,若
,若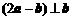 ,则实数
,则实数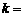 ▲ .
▲ .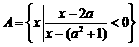 ,
,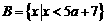 ,若
,若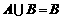 ,则实数
,则实数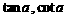 分别是关于
分别是关于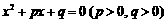 的两实根的等差中项和等比中项,则
的两实根的等差中项和等比中项,则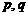 满足的关系式为 ▲ .
满足的关系式为 ▲ .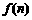 为
为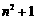 的各位数字之和
的各位数字之和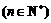 .如:因为
.如:因为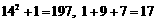 ,所以
,所以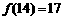 .记
.记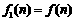 ,
,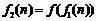 ,……,
,……,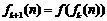 ,
,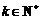 ,则
,则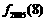 = ▲ .
= ▲ . 直线
直线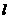 经过抛物线
经过抛物线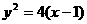 的焦点,且与准线成30
的焦点,且与准线成30 角,则直线
角,则直线 :
: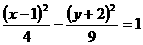 ,给出以下四个命题:
,给出以下四个命题: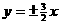 ;
;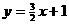 与双曲线
与双曲线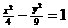 向左平移一个单位,并向上平移两个单位,可以得到双曲线
向左平移一个单位,并向上平移两个单位,可以得到双曲线 其中所有正确命题的序号是
其中所有正确命题的序号是