0 47271 47279 47285 47289 47295 47297 47301 47307 47309 47315 47321 47325 47327 47331 47337 47339 47345 47349 47351 47355 47357 47361 47363 47365 47366 47367 47369 47370 47371 47373 47375 47379 47381 47385 47387 47391 47397 47399 47405 47409 47411 47415 47421 47427 47429 47435 47439 47441 47447 47451 47457 47465 447348
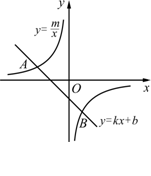 (2007四川资阳)如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数
(2007四川资阳)如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数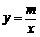 的图象的两个交点.
的图象的两个交点. 3(2007四川成都)如图,一次函数
3(2007四川成都)如图,一次函数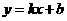 的图象与反比例函数
的图象与反比例函数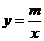 的图象交于
的图象交于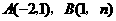 两点.
两点. 的面积.
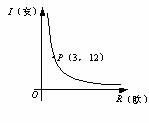
的面积.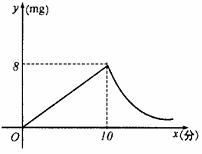 例题. (2008四川巴中市)为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量
例题. (2008四川巴中市)为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量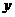 (mg)与燃烧时间
(mg)与燃烧时间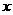 (分钟)成正比例;燃烧后,
(分钟)成正比例;燃烧后, 本题中含药量
本题中含药量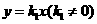 ,由题意点(10,8)在图象上,所以
,由题意点(10,8)在图象上,所以 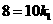
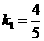 .
. 此阶段函数解析式为
此阶段函数解析式为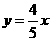
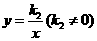 ,由题意 (10,8)在图象上所以
,由题意 (10,8)在图象上所以
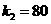 .
.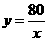
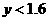 时,得
时,得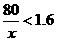
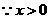
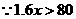
 [针对训练]
[针对训练]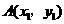 和点
和点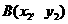 是直线
是直线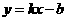 上的两点,且当
上的两点,且当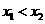 时,
时,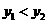 ,那么函数
,那么函数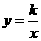 的图象大致是( )
的图象大致是( )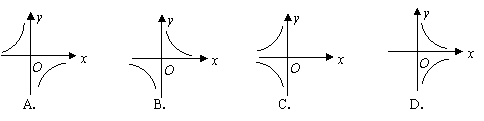

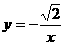 图象上的两个点,且a1<a2,则b1与b2的大小关系是( )
图象上的两个点,且a1<a2,则b1与b2的大小关系是( )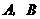 两点,与
两点,与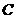 ,与
,与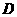 ,
,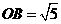 .且点
.且点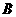 横坐标是点
横坐标是点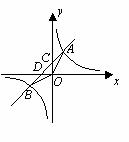 (1)求反比例函数的解析式;
(1)求反比例函数的解析式; 横坐标为
横坐标为 ,
, 面积为
面积为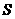 ,求
,求 思路点拨:反比例函数常与一次函数结合,利用一次函数求反比例函数,利用反比例函数性质求一次函数,或两者结合一起解决问题,本题利用B点的坐标的特征求出反比例函数,再根据反比例函数求一次函数解析式,进而求出
思路点拨:反比例函数常与一次函数结合,利用一次函数求反比例函数,利用反比例函数性质求一次函数,或两者结合一起解决问题,本题利用B点的坐标的特征求出反比例函数,再根据反比例函数求一次函数解析式,进而求出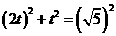 ,解得t =-1。
,解得t =-1。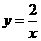 。
。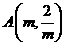 、
、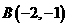 得
得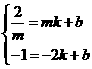 ,解得
,解得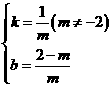 ,所以函数解析式为
,所以函数解析式为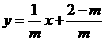
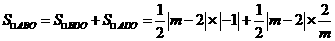
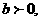 所以有
所以有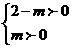 或
或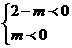 ,解得
,解得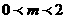 ,
,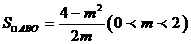 。
。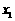 ,
,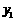 )、B(
)、B(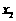 ,
,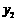 )在函数
)在函数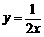 的图象上,则当
的图象上,则当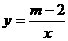 的图象,那么实数
的图象,那么实数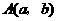 ,
,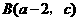 两点均在函数
两点均在函数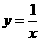 的图象上,且
的图象上,且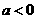 ,则
,则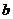 与
与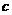 的大小关系为( )
的大小关系为( ) A.
A.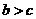 B.
B.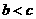 C.
C.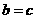 D.无法判断
D.无法判断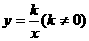 ,当
,当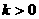 ,对于每一个分支,y随x的增大而减小;当
,对于每一个分支,y随x的增大而减小;当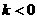 ,对于每一个分支,y随x的增大而增大.
,对于每一个分支,y随x的增大而增大.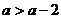 ,
,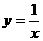 ,
,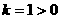 ,在每个分支上y随x的增大而减小,所以
,在每个分支上y随x的增大而减小,所以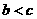 ,选 B .
,选 B .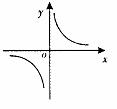 (2008甘肃兰州)若反比例函数
(2008甘肃兰州)若反比例函数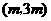 ,其中
,其中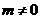 ,则此反比例函数的图象在( )
,则此反比例函数的图象在( )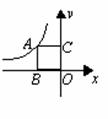 (2008浙江宁波)如图,正方形
(2008浙江宁波)如图,正方形 的边长为2,反比例函数
的边长为2,反比例函数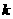 的值是( )
的值是( )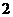 B.
B.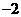 C.
C.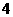 D.
D.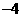
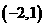 在它的图像上
B.它的图像经过原点
在它的图像上
B.它的图像经过原点 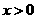 时,
时, 思路点拨:反比例函数
思路点拨:反比例函数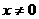 ;
;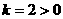 ,函数的两个分支在第一 三象限,所以答案C 是正确的;而
,函数的两个分支在第一 三象限,所以答案C 是正确的;而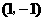 的反比例函数解析式是( )
的反比例函数解析式是( )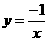 C.
C.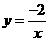
 例题。(2007南充)已知反比例函数的图象经过点(3,2)和(m,-2),则m的值是__.
例题。(2007南充)已知反比例函数的图象经过点(3,2)和(m,-2),则m的值是__.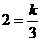 ,解得
,解得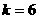 ,所以反比例函数的解析式为
,所以反比例函数的解析式为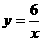 ,而点(m,-2)也在函数图象上,代入得,
,而点(m,-2)也在函数图象上,代入得,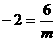 ,
,