摘要:如图.已知A.B(n.-4)是一次函数y=kx+b的图象与反比例函数的图象的两个交点. (1) 求此反比例函数和一次函数的解析式, (2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围. 3如图.一次函数的图象与反比例函数的图象交于两点. (1)试确定上述反比例函数和一次函数的表达式, (2)求的面积. 考点五 反比例函数的应用. 例题. 为预防“手足口病 .某校对教室进行“药熏消毒 .已知药物燃烧阶段.室内每立方米空气中的含药量(mg)与燃烧时间成正比例,燃烧后.与成反比例.现测得药物10分钟燃完.此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题: (1)求药物燃烧时与的函数关系式. (2)求药物燃烧后与的函数关系式. (3)当每立方米空气中含药量低于1.6mg时.对人体方能无毒害作用.那么从消毒开始.经多长时间学生才可以回教室? 思路点拨:利用反比例函数解决实际问题.首先根据题目中所给条件 求出反比例函数的解析式.在利用反比例函数的性质解决相关问题. 本题中含药量与燃烧时间之间的关系是由两个部分组成.要分别求出.由特殊点容易求出两个函数的解析式.再根据反比例函数的性质求出学生回教室的时间. 解析:(1)设药物燃烧阶段函数解析式为.由题意点在图象上.所以 .此阶段函数解析式为 (2)设药物燃烧结束后的函数解析式为.由题意 在图象上所以 .此阶段函数解析式为 (3)当时.得 从消毒开始经过50分钟后学生才可回教室. 规律总结:反比例函数的应用问题关键是先根据问题中的条件求出反比例函数的解析式.再用函数性质解决问题.待定系数法仍然是求函数解析的常用方法. [针对训练]
网址:http://m.1010jiajiao.com/timu3_id_473690[举报]
 23、如图:已知△ABC与△DEF是一副三角板的拼图,A,E,C,D在同一条线上.
23、如图:已知△ABC与△DEF是一副三角板的拼图,A,E,C,D在同一条线上. 如图:已知△ABC与△DEF是一副三角板的拼图,A,E,C,D在同一条线上.
如图:已知△ABC与△DEF是一副三角板的拼图,A,E,C,D在同一条线上.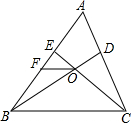 如图,已知D、E是AC、AB上的点,BD、CE交于O点,过O点作OF∥CB交AB于F,AD=
如图,已知D、E是AC、AB上的点,BD、CE交于O点,过O点作OF∥CB交AB于F,AD=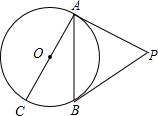 如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC的度数是( )
如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC的度数是( )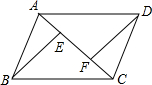 (2013•市中区二模)如图,已知E,F是四边形ABCD对角线AC上的两点,AE=CF,BE=FD,BE∥FD.
(2013•市中区二模)如图,已知E,F是四边形ABCD对角线AC上的两点,AE=CF,BE=FD,BE∥FD.