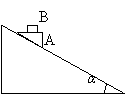|
13. 解: 将两物体看作整体,根据牛顿第二定律计算沿斜面下滑加速度: a= 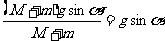 ①(2分) ①(2分)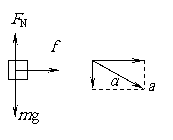 单独分析物体m,受力分析如图: 单独分析物体m,受力分析如图:水平方向上根据牛顿第二定律: f=macosα ②(2分) 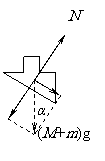 竖直方向上根据牛顿第二定律: 竖直方向上根据牛顿第二定律:mg-FN=masinα ③(2分) 由①②③式解得: FN=mg-mg sin2α f=mg sinα cosα f为静摩擦力,应不大于最大静摩擦力,有: f ≤ μFN ④(2分) 代入结果化简可得: μ ≥ tanα ⑤(2分) 注:高一数学三角函数公式未学,结果可能为 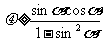 |
|
14. 解: 物块在地面上减速滑行的加速度为: a=gμ=2m/s2 (2分) 物块停下来应花时间: t= 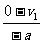 = =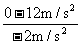 =6s =6s滑行距离: s= 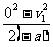 = =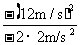 =36m
(2分) =36m
(2分)而在此时间内小球平抛运动水平方向位移为: x=v2t=4m/s×6s=24m 所以在物块停止滑行时,在水平方向上小球仍未能追上物块,因此只要小球平抛运动的射程等于物块的滑行距离,即能击中物块。(4分) 因此小球平抛运动所花时间: t´= 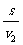 = =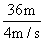 =9s
(2分) =9s
(2分)平抛运动下落高度为: h= 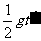 = =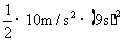 =405m (2分) =405m (2分)小球应从A点上方405m处抛出。 |
|
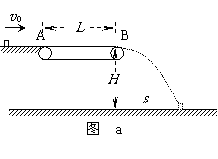
15. 解: 物体受滑动摩擦力产生加速度大小为: a=gμ=2m/s2 若物块一直受到向后的滑动摩擦力减速至B端,速度为v1,则: v12-v02=2(-a)L 得v1=1m/s,此为物块到达B端时所能获得的最小速度。 若物块一直受到向前的滑动摩擦力加速至B端,速度为v2,则: v22-v02=2aL 得v2=7m/s,此为物块到达B端时所能获得的最大速度。 物块离开B端后做平抛运动的时间: t= 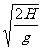 =1s =1s(1) u= -1m/s时,物块一直受向左摩擦力减速到v1,离开B端时速度为v1 s=v1t=1m (3分) (2) u= 0时,物块也将一直受向左摩擦力减速到v1,离开B端时速度为v1 s=v1t=1m (3分) (3) u= 3m/s时,物块减速至3m/s即与传送带相对静止,离开B端时速度为3m/s s=ut=3m (3分) (4) u= 6m/s时,物块加速至6m/s即与传送带相对静止,离开B端时速度为6m/s s=ut=6m (3分) (5) u= 8m/s时,物块一直加速到v2到达B端,离开B端时速度为v2 s=v2t=7m (3分) |
|
16. 解: P刚开始下落到相互作用区边缘时,其速度: v=gT0=20m/s 接下来在相互作用且下落过程中,P的加速度: a= 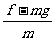 =(a-1)g=500m/s2 =(a-1)g=500m/s2减速下落时间: t0= 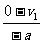 =0.04s
(3分) =0.04s
(3分)P接下来的上升过程为下降过程的逆过程,花时间t0+T0回到最初出发点,以后一直重复此过程。 以P下降上升的一个循环过程时间内来考查B物体,总时间T=2 t0+2 T0。(3分) 在两物体没有相互作用的时间2 T0内,B的滑行加速度: a1=gμ=0.2m/s2 B的速度减小量: Δv1= a1·2 T0=0.8m/s (3分) 在两物体相互作用的时间2 t0内,B的滑行加速度: a2= 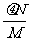 = =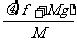 = =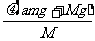 =1.22m/s2 =1.22m/s2B的速度减小量: Δv2= a2·2 t0=0.0976m/s (3分) 所以在P下降上升一次的过程中,B的速度减小量为: Δv=Δv1+Δv2=0.8976m/s 所以在从开始运动到B停下来的时间内,P下降再上升经过的循环次数为: 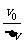 = =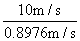 ≈11.14 ≈11.14 所以到B停下那一刻,P回到初始位置11次。(3分) |
本资料由《七彩教育网》 提供!
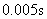 内由
内由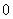 增加到
增加到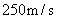 ,这里的速度表示的是平均速度
,这里的速度表示的是平均速度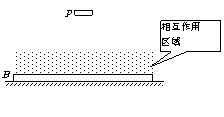
 (1) u= -1m/s;
(1) u= -1m/s;