5.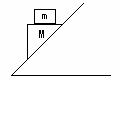 如图所示,木块M上表面是水平的,当小木块m置于M上,并与M一起沿摩擦因数为μ倾角为θ的斜面由静止开始下滑,在下滑过程中,求:(1)m与M一起下滑的加速度?(2)M对m的的支持力和摩擦力大小?
如图所示,木块M上表面是水平的,当小木块m置于M上,并与M一起沿摩擦因数为μ倾角为θ的斜面由静止开始下滑,在下滑过程中,求:(1)m与M一起下滑的加速度?(2)M对m的的支持力和摩擦力大小?
解:(1)
|
(2)f=macosθ,mg-Fn=masinθ.
f=m cosθ(gsinθ-μgcosθ),Fn= mg-msinθ(gsinθ-μgcosθ)
5. 如图所示,木块M上表面是水平的,当小木块m置于M上,并与M一起沿摩擦因数为μ倾角为θ的斜面由静止开始下滑,在下滑过程中,求:(1)m与M一起下滑的加速度?(2)M对m的的支持力和摩擦力大小?
如图所示,木块M上表面是水平的,当小木块m置于M上,并与M一起沿摩擦因数为μ倾角为θ的斜面由静止开始下滑,在下滑过程中,求:(1)m与M一起下滑的加速度?(2)M对m的的支持力和摩擦力大小?
解:(1)
|
(2)f=macosθ,mg-Fn=masinθ.
f=m cosθ(gsinθ-μgcosθ),Fn= mg-msinθ(gsinθ-μgcosθ)