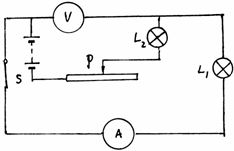
[思维基础]
电功就是电流通过用电器做的功。电流做功过程实际就是电能转化为其他形式的能的过程。电流做了多少功,就有多少电能转化为其它形式的能。
电流在某段电路上所做的功,等于这段电路两端的电压,电路中的电流和通电时间的乘积。即
W=UIt
电功的主单位是焦耳。简称为焦。
1焦耳=1牛顿·米=1伏×1安×1秒。
焦耳这个单位很小,平时常用度做电功单位。1度=3.6×106焦。
应用W=UIt公式时,特别要注意的是U和I是加在同一个用电器两端电压和电流。
例题1 一个电热器所用的电压是220伏,电流是0.2安,通电时间为10分钟。电流做的功是 焦。
分析:根据电功的计算公式图3
W=UIt
=220伏×0.2安×10×60秒
=26400焦
答:此题应填26400 。
例题2 用一节1.5伏的干电池点燃小灯泡,通过小灯泡的电量是14库,则电流做的功是 焦。
分析:此题未给出通过小泡泡的电流I和通电时间t,但给出了通过小灯泡的电量Q,因为电流I=Q/t,所以
Q=It
电流做的功
W=UIt
=UQ
=1.5伏×4库
=21焦
所以,电功的单位也可以是
1焦=1伏×1库
答:此题应填21 。
例题3 电路中一导体上的电压为2伏,导体中的电流为0.2安,若电流做功是24焦,则通电时间是 秒。
 分析:电功的计算公式
分析:电功的计算公式
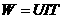
可知,通电时间为
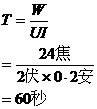
 答:此题应填 60 。
答:此题应填 60 。
电流在单位时间内所做的功叫做电功率。电功率是表明电流做功快慢的物理量。
电功率等于电压和电流的乘积。
即 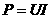
电功率的单位是瓦特,简称为瓦。电功率的单位还有千瓦。1千瓦=1000瓦。
电功率为1千克,电流在1小时内所做的功就是1千瓦时,千瓦时也就是前面提到的“度”。
1千瓦时=1000瓦×3600秒
=3.6×106焦
用电器上标着的电压值是用电器正常工作时的电压,叫额定电压。用电器上标着的功率值是用电器在额定电压的电功率,叫额定功率。应该特别注意的是,如果用电器两端的电压不等于它的额定电压,它的实际电功率也就不等于它的额定功率。
例题4 加在一个标有“220V、40W”的灯泡上的电压为200伏,通过的电流是0.165安,则这个灯泡的额定功率是 瓦,实际功率是 瓦。
分析:灯泡上已标明了它的额定电压是220伏,额定功率是40瓦。它的实际功率
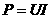
=200伏×0.165安
=33瓦
答:此题应填 40 、33 。
例题5 实际小组自制一把“220V、22W”的电烙铁,在额定电压下使用,通过电烙铁的电流是 安。
分析:由电功率的公式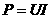 可知,所求电流为
可知,所求电流为
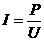
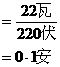
答:此题应填0.1 。
例题6 标有:“220V、800W”的一个电炉正常工作2小时,消耗的电能是 千瓦时。
分析:此电炉的额定功率是0.8千瓦,正常工作2小时所做电功
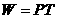
=0.8千瓦×2小时
=1.6千瓦时
答:此题应填1.6 。
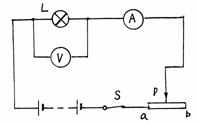
测定小灯泡的功率的实验。一般是用图9-3的电路来测定小灯泡的额定功率。
|
图9-3 |
例题7 用电流表和电压表测定小灯泡的额定功率。实验有如下几个步骤:
(A)合上电键;
(B)使滑动变阻器的阻值调到最大;
(C)按电路图连接电路(注意选择电表量程);
(D)记下电流表和电压表的示数;
(E)调节滑动变阻器的阻值,使电压表的示数
达到小灯泡的额定电压值。
请把以上步骤前的字母,按照合理的顺序 填入下面空白处。
① ,② ,③ ,④ ,⑤ 。
分析:连接好电路,在开关闭合前,为了不损坏仪器要先将滑动变阻器的阻值调到最大;还要检查电流和电压表在电路中连接的是否正确,所选量程是否合适。
在测量小灯泡的额定功率时,需用滑动变阻器调节小灯泡两端的电压,使之达到额定电压。
答:此题应填① C ,② B ,③ A ,④ E ,⑤ D 。
电流流过导体产生的热量,跟电流的二次方成正比,跟导体的电阻成正比,跟通电的时间成正比。这个规律叫做焦耳定律。公式是
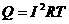
热量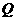 的单位是焦耳。
的单位是焦耳。
电热器是利用电流的热效应制成的加热设备。电热器的主要组成部分是发热体。发热体是电阻大、熔点高的合金丝绕在绝缘材料上做成的。
例题8 某导体的电阻为5欧,当通过2安的电流时,30秒内这个导体产生的热量是
焦。
分析:由焦耳定律知导体产生的热量
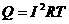
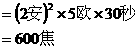
答:此题应填600 。
[经典题解]
[电功]
例题1 串联在照明电路里的两盏电灯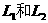 ,如果
,如果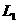 的电阻比
的电阻比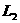 电阻大,那么
电阻大,那么
在相等的时间内,电流通过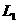 所做的功
所做的功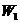 和通过
和通过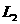 所做的功
所做的功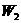 相比是( )
相比是( )
(A)W1>W2 (B)W1=W2
(C)W1<W2 (D)无法确定
分析:电流通过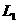 所做的功
所做的功
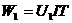
电流通过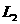 所做的功
所做的功
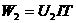
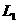 和
和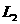 串联,通过两灯里的电流
串联,通过两灯里的电流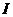 相同。因电阻
相同。因电阻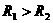 ,而串联电路里各个电阻两
,而串联电路里各个电阻两
端的电压跟它的阻值成正比,所以
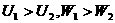
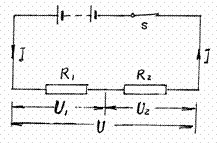
答:此题应选(A)。例题2 有两个电阻,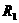 =100欧,
=100欧,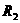 =140欧,把它们串联后,接在24伏的电源上经1分钟。电流通过
=140欧,把它们串联后,接在24伏的电源上经1分钟。电流通过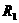 做的功
做的功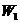 = ,电流通过
= ,电流通过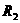 所做的功
所做的功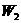 = ,
= , 。(图9-4)
。(图9-4)
分析:电流通过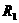 做的功
做的功
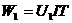
根据欧姆定律
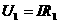
因此,电流通过R1所做的功又可
表示为
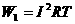 ①
①
R1与R2组成串联电路,其总电阻
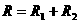
=240欧
电路里的电流
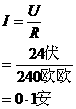
将电流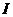 的值和
的值和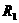 的值代入①式
的值代入①式
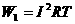
=(0.1安)2×100欧×60秒
=60焦
同法求电流通过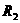 所做的功
所做的功
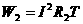 ②
②
=(0.1安)2×140欧×60秒
=84焦
电功之比由①式与②式联立求得
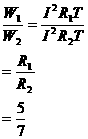
这说明在串联电路中,电功按电阻成正比的进行分配。
答:此题应填60焦,84焦,5∶7。
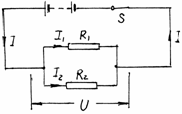 例题3 两个电阻,
例题3 两个电阻,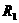 =100欧,
=100欧,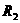 =140欧,把它们并联后,接在24伏的电源上,经过1分钟,电流通过
=140欧,把它们并联后,接在24伏的电源上,经过1分钟,电流通过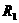 所做的功
所做的功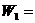 ,电流通过
,电流通过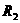 所做的功
所做的功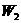 = ,
= ,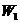 :
: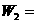 。(图9-5)
。(图9-5)
分析:电流通过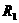 所做的功
所做的功
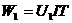
根据欧姆定律
|
图9-5 |
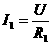
因此,电流通过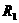 所做的功又可表示为
所做的功又可表示为
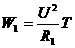 ①
①
=(24伏)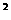
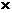 100欧×60秒
100欧×60秒
=345.6焦
同法求电流通过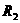 所做的功
所做的功
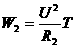 ②
②
=(24伏)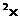 140欧×60秒
140欧×60秒
=246.9焦
电功之比由①式与②式联立求得
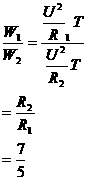
这说明在并联电路中,电功按电阻成反比的进行分配。
答:此题应填345.6焦,246.9焦,7∶5。
[电功率]
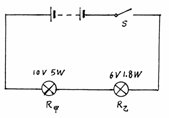
例题4 一只“10V、5W”的甲灯和一只“6V、1.8W”的乙灯串联后接入电路中,两灯均能发光,比较它们的实际功率(不考虑灯丝电阻随温度的变化)( )图9-6。
(A)甲灯大些 (B)乙灯大些
(C)两灯一样大 (D)无法确定
 分析:由欧姆定律结合电功率的知识,可知电功率的计算公式还可以改写成
分析:由欧姆定律结合电功率的知识,可知电功率的计算公式还可以改写成
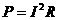 ①
①
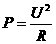 ②
②
先用②式,依照灯泡的额定电压和额定功率,找出
( 图 9-6 ) 甲灯和乙灯的电阻是一定不变的。
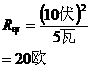
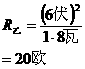
因两灯串联,通过它们的电流相同,再由两灯电阻相同,依公式①来考虑,甲、乙两灯的实际功率应一样大。
答:此题应选(C)。
例题5 把标有“9V、9W”的甲灯和标有“6V、1W”的乙灯,串联在15伏的电源上,下列说法中正确的是( )
(A)两灯都能正常发光
(B)只有乙灯能正常发光
(C)只有甲灯能正常发光
(D)有可能两灯均不能正常发光
分析:根据两灯的额定电压和额定功率求出两个灯的电阻
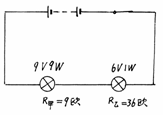
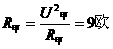
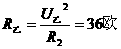
(图 9-7)
两灯串联在15伏的电源上,因两灯的电阻之比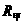 ∶
∶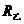 =1∶4,两灯实际分配的电压
=1∶4,两灯实际分配的电压
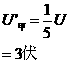
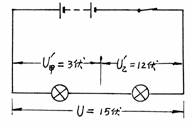
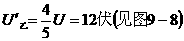
(图 9-8 )
两灯实际功率
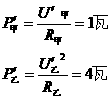
计算结果甲灯实际功率小于额定功率,乙灯实际功率是其额定功率的4倍。两灯均不能正常发光,且乙灯丝可能被烧断。因此,选项(D)是唯一正确的。
答:此题应选(D)。
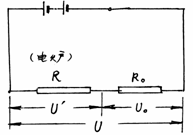
例题6 一台标有“200V、400W”的电炉子,接在电源上,电炉恰能正常工作。现要使电炉子的功率降为额定功率的一半,应给电炉子串联一个多大的电阻后,再接在电源上(电炉丝电阻不变)( )
 (A)100欧 (B)50欧
(A)100欧 (B)50欧
(C)41.4欧 (D)82.8欧
分析:电炉子的电阻,可由其额定电压和额定电阻求出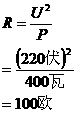

( 图 9-8 )
串联电阻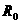 后电路如图9-8所示。设此时
后电路如图9-8所示。设此时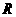 与
与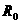 分配的电压为U′与
分配的电压为U′与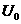 ,依题意此时电炉子的实际功率
,依题意此时电炉子的实际功率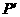 为其额定功率的一半,即为200瓦。
为其额定功率的一半,即为200瓦。
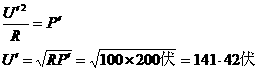
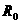 上分配的电压
上分配的电压
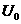 =200伏-141.42伏
=200伏-141.42伏
=58.58伏
因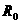 与R组成的串联电路,在串联电路中电压按电阻成正比分配。因此,串联的电阻
与R组成的串联电路,在串联电路中电压按电阻成正比分配。因此,串联的电阻
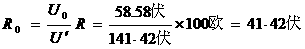
答:此题应选(C)。
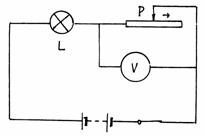
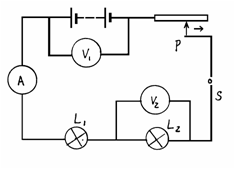
例题7 在图9-9所示电路中,电路两端电压不变,当滑动变阻器滑片P向右滑动时( )
 (A)电压表示数变大,灯L变亮
(A)电压表示数变大,灯L变亮
(B)电压表示数变小,灯L变暗
(C)电压表示数变大,灯L变暗
(D)电压表示数变小,灯L变亮
分析:滑动变阻器的滑片P向右滑动,它的阻值增大。
滑动变阻器与L灯组成串联电路,在串联电路中,
( 图 9-9 ) 电压按电阻成正比的进行分配。当滑动变阻器电阻增大 时,它两端的电压亦增大。所以,电压表示数应变大。(B)、(C)两选项可以排除。
 滑片向右移,使电路的总电阻变大,根据欧姆定律可知电路里的电流应变小。电灯的电阻是不变的,由P=I2R来判断,灯的实际功率将变小,灯会变暗。(A)选项亦被排除。
滑片向右移,使电路的总电阻变大,根据欧姆定律可知电路里的电流应变小。电灯的电阻是不变的,由P=I2R来判断,灯的实际功率将变小,灯会变暗。(A)选项亦被排除。
答:此题应选 C 。
例题8 如图9-10所示的电路,电源电压不变。试用“变大、变小、变亮、变暗、变为0、不变”回答下列问题:
(1)当滑片向右滑动时,电压表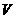
 的示数,电压表的示数,电流表
的示数,电压表的示数,电流表 的示数,灯
的示数,灯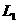 和
和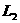 的亮度 。
的亮度 。
|
( 图 9-10 ) |
(2)当开关S断开时,电压表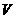
 的示数 ,电压表
的示数 ,电压表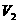 的示数
。
的示数
。
分析:由于电源电压不变,V1的示数也就不变。滑动变阻器与灯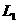 、
、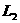 组成串联电路,当滑片向右滑动时,电路的总电阻变大,根据欧姆定知电路里电流变小。因此,电流表A的示数将变小。
组成串联电路,当滑片向右滑动时,电路的总电阻变大,根据欧姆定知电路里电流变小。因此,电流表A的示数将变小。
两灯电阻不变,当电流变小时,灯上的电压,灯的实际功率,依照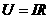 和
和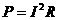 这两个公式判断,都将变小。即两灯要变暗,与
这两个公式判断,都将变小。即两灯要变暗,与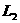 灯并联的电压表
灯并联的电压表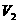 示数要变小。
示数要变小。
当开关S断开时,电路处于开始状态,电压表示数仍不变,电压表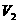 示数为0 。
示数为0 。
答:此题应填(1)不变,变小,变小,变暗;(2)不变,为零。
[测定小灯泡的功率]
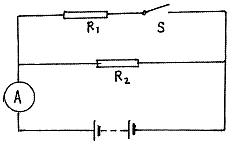
例题9 为了测定电压为2.5伏的小灯泡的额定功率。
(1)在图9-11上标出电流表和电压表,并标明“+”、“-”接线柱的符号。
(2)在开关闭合前,滑动变阻器的滑片P应移到a端还是b端? 端。
(3)若电源由两节干电池组成,所用电流表的量程有0.6安和3安;电压表的量程有3伏和15伏。估计小灯泡的电阻为8欧左右,那么电流表的量程( 图 9- 11)应选 ,电压表的量程应选 。
(4)记录下 和 的示数,应用公 式 ,计算出小灯泡的额定功率。
分析:电路图画完整后应如图9-11所示。“+”、“-”接线柱的符号已在电表上标注清楚。
因电源电压为3伏,灯泡电阻为8欧左右,所以电路里最大的电流值约为0?38安。电流表量程应稍大于0.38安。故电流表量程选0.6安,电压表量程选3伏。4
答:此题应填(2)b,(3)0?6安,3伏,(4)电压表,电流表,P=UI。
[焦耳定律]
 例题10 如图9-12所示,电路两端电压保持不变,电阻R1=60欧,电阻R2=40欧,当开关S断开时,电流表示数为0.3安,则开关S闭合后,50秒内电流通过两电阻产生的热量总共是 焦。
例题10 如图9-12所示,电路两端电压保持不变,电阻R1=60欧,电阻R2=40欧,当开关S断开时,电流表示数为0.3安,则开关S闭合后,50秒内电流通过两电阻产生的热量总共是 焦。
分析:当开关S断开时,电路里只有R2一个电阻,这时电路两端电压
U=IR2
=0.3安×40欧
=12伏
当开关S闭合后,电阻R1和R2组成并联电路。电路的总电阻为
R=R1R2 R1+R2
( 图 9-12 ) =60欧×40欧 60欧+40欧
=24欧
这时干路里电流为
I=UR
=12伏 24欧
 =0.5安
=0.5安
电流通过两电阻产生的热量
Q=I2Rt
=(0.5安)2×24欧×50秒
=300焦
答:此题应填300 。
( 图 9-13 )
[思维体操]
下面选几个电功率与欧姆定律的综合题来分析一下。这类题有一定难度,但对培养思维能力和提高学习成绩有着重要意义。
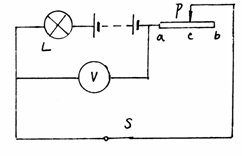
例题1 如图9-13所示的电路中,电源电压保持不变,变阻器滑片P滑到C点时,电压表为4伏,灯L正常发光;当滑片P滑到b点时,电压表示数为8伏。已知灯L的电阻为4欧,电阻Rac=1 4Rab,则灯L的额功率是
(A)16瓦 (B)8瓦
(C)4瓦 (D)2瓦
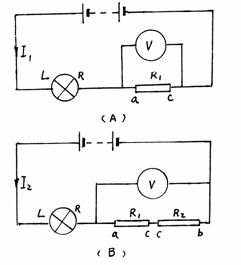 分析:当变阻器滑片在C点时,灯L与变阻器ac之间的电阻R1串联,其等效电路如图9-14(A)。
分析:当变阻器滑片在C点时,灯L与变阻器ac之间的电阻R1串联,其等效电路如图9-14(A)。
根据欧姆定律知图(A)电路中电流
I1=U R+R1
电压表与R1并联,量度的R1两端电压U1,U1=4伏
I1R1=U1
由上面二个公式可得(注意灯L电阻R=4欧)
U 4+R1×R1=4 ①
滑片P滑到b点时,灯L电阻R与滑动变阻器ab之间的电阻(R1+R2)串联,其等效电路如图(B)所示。由题意知 R1+R2 等于
( 图 9-14) 4R1,根据欧姆定律
I2=U R+4R1
电压表与(R1+R2)并联,量度的滑动度阻上的电压,此电压U2=8伏
I2 (R1+R2)=U2
由上二式可得
U 4+4R1·4R1=8 ②
由①与②式联立解得变阻器ac段电阻
R1=2欧
再由图(A)的情况来分析,灯L此时正常发光,灯L与R1串联,串联电路中电压按电阻成正比进行分配,故灯L两端电压U2可用下式求出
 U2 R=U1 R1
U2 R=U1 R1
U2 =R R1·U1
=4欧 2欧×4伏
=8伏
灯L的额定功率
P=U2L R
=(8伏)2 4欧
=16瓦
( 图 9-15 )
答:此题应选(A)。
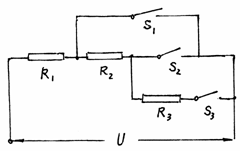
例题2 如图9-15所示电路,电路两端电压保持不变,当只闭合开关S1时,通过电阻R1的电流是I1;当只闭合开关S2时,通过电阻R2的电流为I2,电阻R2消耗的功率为20瓦,I1∶I2=3∶2;当只闭合开关S3时,电阻R3消耗的功率是15瓦。
求:(1)只闭合S1时,R1消耗的功率。
( 图 9-15 ) (2)只闭合S3时,R1消耗的功率。
分析:(1)只闭合S1时,电路中只有R1中有电流,根据欧姆定律
I1=U R ①
由电功率的公式
P1=I21R1 ②
只闭合S2时,电阻R1与R2串联,根据欧姆定律
I2=U R1+R2 ③
由电功率的公式,电阻R1消耗的功率
P′1=I23R1 ④
因题目给出I1∶I2=3∶2,由①式与③式得出
I1 I2=R1+R2 R2=3 2
即R1=2R2
在只关闭S2时,R1与R2串联,而串联电路中电功率按电阻成正比分配。这时R2的电功率为20
瓦,电阻R1上的电功率
P′1=40瓦
再由②式和④式联立
P1 P′1=I21R1 I22R1
=(I1 I2)2
=(3 2)2
=9 4
P1=9 4×P′1
=90瓦
求P1的另种解法为得出R1=2R2后,先写电阻R2的电功率的式子
P2=(U R1+R2)2 R2=20瓦
∴ P1 P2=(R1+R2 R1)2 R1 R2=9 2
P1=92 P2=9 2×20瓦=90瓦
(2)因R1=2R2,在只闭合S2时,有
(U 3R2)2R2=20瓦 ⑤
在只闭合S3时,有
(U 3R2+R3)2·R3=15瓦 ⑥
由⑤式与⑥式联立得
(3R2+R3)2 9R2·R2 R3=4 3
代简并整理
R23-6R2R3+9R22=0
即R3=3R2
前已得出R1=2R2,∴R3=32R1,在只闭合S3时,R1的电功率P″1可由下式算出
P″1 R1=P3 3 2R1
P″1=2 3P3
=2 3×15瓦
=10瓦
答:(1)只闭合S1时,R1消耗的功率为90瓦;(2)只闭合S3时,R1消耗的功率为10瓦。
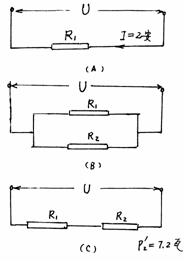
例题3 把电阻R1接入电压保持不变的电路中,通过R1的电流为2安,R1消耗的电功率设为P1。把电阻R2与R1并联后接入该电路中,电路消耗的总功率设为P2,且P2=2?5P1。若把R1和R2串联后仍接入该电路中,电阻R2消耗的电功率为7.2瓦,则电阻R1的阻值是 欧。
分析:按题意画出三种情况的电路如图9-16所示。在图(A)的情况下,根据欧姆定律和电功率的公式
I=U R1 ①
 P1=U2
R1
②
P1=U2
R1
②
在图(B)的情况下
P2=U2 R1R2 R1+R2 ③
依题意有
P2=2.5P1 ④
由②③④式联立得出
R2 R1+R2=1 2.5
R1+R2=2.5R2
或 R2=2 3R1
在图(C)情况下,电阻R2的电功率
(U 2.5R2)2·R2=7.2瓦 ⑥
由①式及题给条件I=2安可得出 ( 图 9-16 )
U2=4R21 ⑦
由⑥式与⑦式联立解得(注意R2=2 3R1)
R1=7.5欧
答:此题应填7.5。