0 135405 135413 135419 135423 135429 135431 135435 135441 135443 135449 135455 135459 135461 135465 135471 135473 135479 135483 135485 135489 135491 135495 135497 135499 135500 135501 135503 135504 135505 135507 135509 135513 135515 135519 135521 135525 135531 135533 135539 135543 135545 135549 135555 135561 135563 135569 135573 135575 135581 135585 135591 135599 447348
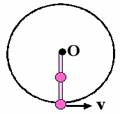 例1、如图示,长为l 的轻质硬棒的底端和中点各固定一个质量为m的小球,为使轻质硬棒能绕转轴O转到最高点,则底端小球在如图示位置应具有的最小速度v= 。
例1、如图示,长为l 的轻质硬棒的底端和中点各固定一个质量为m的小球,为使轻质硬棒能绕转轴O转到最高点,则底端小球在如图示位置应具有的最小速度v= 。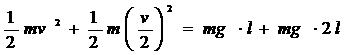 因为小球转到最高点的最小速度可以为0 ,所以,
因为小球转到最高点的最小速度可以为0 ,所以,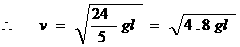
 解:对系统由机械能守恒定律
解:对系统由机械能守恒定律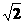 两个小圆环间绳子的中点C处,挂上一个质量M= m的重物,使两个小圆
两个小圆环间绳子的中点C处,挂上一个质量M= m的重物,使两个小圆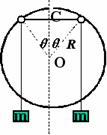 环间的绳子水平,然后无初速释放重物M.设绳子
环间的绳子水平,然后无初速释放重物M.设绳子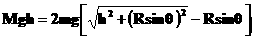
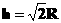 解得
解得 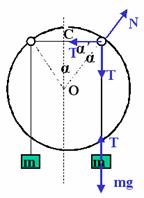 d.除上述三种情况外,根据对称性可知,系统如能平衡,则两小圆环的位置一定关于大圆环竖直对称轴对称.设平衡时,两小圆环在大圆环竖直对称轴两侧α角的位置上(如图所示).
d.除上述三种情况外,根据对称性可知,系统如能平衡,则两小圆环的位置一定关于大圆环竖直对称轴对称.设平衡时,两小圆环在大圆环竖直对称轴两侧α角的位置上(如图所示).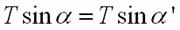
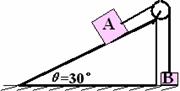
 例 4. 如图质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态。一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩。开始时各段绳都牌伸直状态,A上方的一段沿竖直方向。现在挂钩上挂一质量为m3的物体C上升。若将C换成另一个质量为(m1+m3)物体D,仍从上述初始位置由静止状态释放,则这次B则离地时D的速度的大小是多少?已知重力加速度为g。
例 4. 如图质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态。一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩。开始时各段绳都牌伸直状态,A上方的一段沿竖直方向。现在挂钩上挂一质量为m3的物体C上升。若将C换成另一个质量为(m1+m3)物体D,仍从上述初始位置由静止状态释放,则这次B则离地时D的速度的大小是多少?已知重力加速度为g。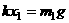
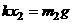

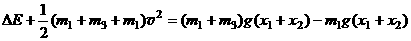
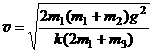
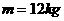 的静止物体P,弹簧的劲度系数
的静止物体P,弹簧的劲度系数 。现施加给P一个竖直向上的拉力F,使P从静止开始向上做匀加速运动。已知在头0.2s内F是变力,在0.2s以后,F是恒力,取
。现施加给P一个竖直向上的拉力F,使P从静止开始向上做匀加速运动。已知在头0.2s内F是变力,在0.2s以后,F是恒力,取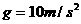 ,求拉力F的最大值和最小值。
,求拉力F的最大值和最小值。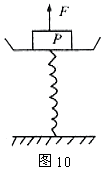
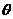 的长斜面上有一带风帆的滑块,从静止开始沿斜面下滑,滑块质量为m,它与斜面间的动摩擦因数为
的长斜面上有一带风帆的滑块,从静止开始沿斜面下滑,滑块质量为m,它与斜面间的动摩擦因数为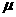 ,帆受到的空气阻力与滑块下滑速度的大小成正比,即
,帆受到的空气阻力与滑块下滑速度的大小成正比,即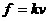 。
。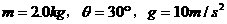 ,从静止下滑的速度图象如图所示的曲线,图中直线是t=0时的速度图线的切线,由此求出
,从静止下滑的速度图象如图所示的曲线,图中直线是t=0时的速度图线的切线,由此求出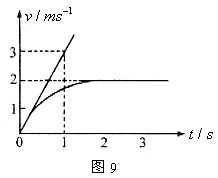
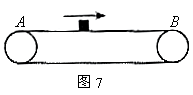
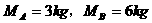 。今用水平力
。今用水平力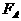 推A,用水平力
推A,用水平力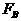 拉B,
拉B,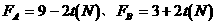 。求从t=0到A、B脱离,它们的位移是多少?
。求从t=0到A、B脱离,它们的位移是多少?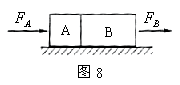
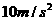 )
)
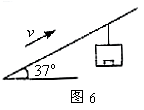
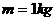 的物体在拉力F作用下沿倾角为30°的斜面斜向上匀加速运动,加速度的大小为
的物体在拉力F作用下沿倾角为30°的斜面斜向上匀加速运动,加速度的大小为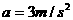 ,力F的方向沿斜面向上,大小为10N。运动过程中,若突然撤去拉力F,在撤去拉力F的瞬间物体的加速度的大小是____________;方向是____________。
,力F的方向沿斜面向上,大小为10N。运动过程中,若突然撤去拉力F,在撤去拉力F的瞬间物体的加速度的大小是____________;方向是____________。