2.受力分析的思路和步骤
2.空间力的受力分
析
3.对摩擦力的正确
理解
弹簧的正确理解
2.整体法和隔法的
灵活选用
①
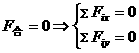
②构成封闭多边形
2.力的合成和分解一平行四边形法则
3.正交分解
2.常用方法:
①合成平衡法
②分解平测法
2.范围分析
①可能性分析
②临界分析
3.极值分析
4.自锁问题
|
板块 |
重要“知识背景” |
疑难问题 |
典型问题 |
|
受力分析 |
1. 静摩擦力与滑动摩擦力 弹力与作用力 0 135346 135354 135360 135364 135370 135372 135376 135382 135384 135390 135396 135400 135402 135406 135412 135414 135420 135424 135426 135430 135432 135436 135438 135440 135441 135442 135444 135445 135446 135448 135450 135454 135456 135460 135462 135466 135472 135474 135480 135484 135486 135490 135496 135502 135504 135510 135514 135516 135522 135526 135532 135540 447348 |
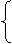 重力与万有引力
重力与万有引力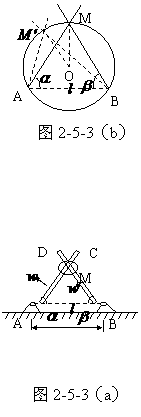 5.2、两杆交点的运动 两杆的交点同时参与了二杆的运动,而且相对每一根杆还有自己的运动,因而是一种比较复杂的运动。
5.2、两杆交点的运动 两杆的交点同时参与了二杆的运动,而且相对每一根杆还有自己的运动,因而是一种比较复杂的运动。 绕A、B两固定轴在同一竖直面内转动,转动方向如图示。当
绕A、B两固定轴在同一竖直面内转动,转动方向如图示。当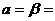 60º,试求t时刻两棒交点M点的速度和加速度。t=0时,△ABM为等边三角形,因此AM=BM=
60º,试求t时刻两棒交点M点的速度和加速度。t=0时,△ABM为等边三角形,因此AM=BM=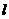 ,它的外接圆半径R=OM=
,它的外接圆半径R=OM=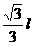 ,图2-5-3(b)。二杆旋转过程中,
,图2-5-3(b)。二杆旋转过程中,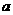 角增大的角度一直等于
角增大的角度一直等于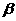 角减小的角度,所以M角的大小始终不变(等于60º),因此M点既不能偏向圆内也不能偏向圆外,只能沿着圆周移动,因为∠
角减小的角度,所以M角的大小始终不变(等于60º),因此M点既不能偏向圆内也不能偏向圆外,只能沿着圆周移动,因为∠ 和∠
和∠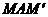 是对着同一段圆弧(
是对着同一段圆弧(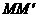 )的圆心角和圆周角,所以∠
)的圆心角和圆周角,所以∠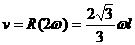
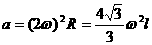
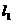 和
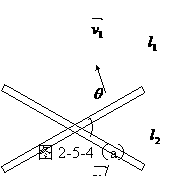
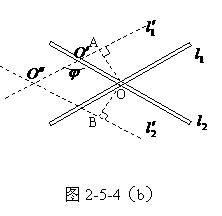
和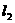 ,各自以垂直于自己的速度
,各自以垂直于自己的速度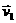 和
和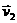 在该平面内运动,试求交点相对于纸平面的速率及交点相对于每根杆的速率。
在该平面内运动,试求交点相对于纸平面的速率及交点相对于每根杆的速率。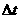 之后,
之后,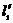 的位置,
的位置,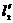 的位置,
的位置, 点,
点, 点。
点。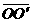 =
=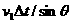
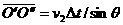
 在
在 中:
中: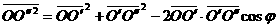
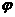 角和
角和 角互补,所以
角互补,所以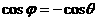
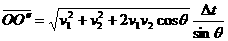
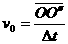
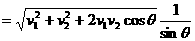
 ,交点相对
,交点相对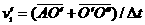
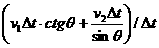
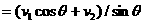
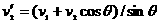
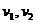 是否为常量无关。如果
是否为常量无关。如果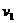 和
和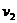 的方向不是与杆垂直,这个问题应该如何解决?读者可以进行进一步的讨论。
的方向不是与杆垂直,这个问题应该如何解决?读者可以进行进一步的讨论。 当绳端在做既不沿绳方向,又不垂直于绳方向的运动时,一般要将绳端的运动分解为沿绳方向和垂直于绳方向二个分运动。
当绳端在做既不沿绳方向,又不垂直于绳方向的运动时,一般要将绳端的运动分解为沿绳方向和垂直于绳方向二个分运动。 着物体m在水平面上运动,A端以速度v做匀速运动,问m做什么运动?有的同学会将绳的速度v分解成竖直
着物体m在水平面上运动,A端以速度v做匀速运动,问m做什么运动?有的同学会将绳的速度v分解成竖直 (u<v).这是错误的。因为实际上木块并没有一个向上的分速度。应该将绳端B实际上的水平速度
(u<v).这是错误的。因为实际上木块并没有一个向上的分速度。应该将绳端B实际上的水平速度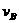 分解成沿绳方向的分速v∥=
分解成沿绳方向的分速v∥=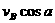 和垂直于绳的分速v⊥=
和垂直于绳的分速v⊥=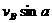 ,v∥使绳子缩短,所以v∥=v,v⊥使绳子围绕滑轮转动。因此
,v∥使绳子缩短,所以v∥=v,v⊥使绳子围绕滑轮转动。因此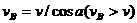 ,而且
,而且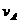 和
和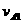 和垂直于杆的分速
和垂直于杆的分速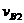 。由于杆的长度不会发生变化,所以
。由于杆的长度不会发生变化,所以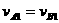 ,即
,即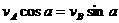 ,即
,即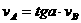
 在竖直方向速度为
在竖直方向速度为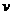 时运动到最高点速度刚好为零,由机械能守恒有
时运动到最高点速度刚好为零,由机械能守恒有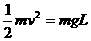
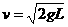
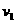 ,此时
,此时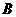 球速度为
球速度为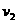 ,且
,且
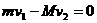
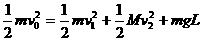
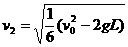
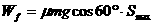
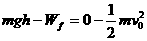
 m
m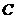 之间的圆弧上来回做变速圆周运动,且在
之间的圆弧上来回做变速圆周运动,且在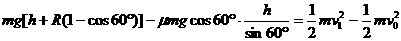
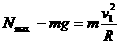
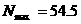 N.
N.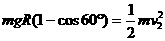
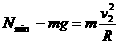
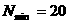 N.
N.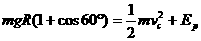
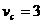 m/s
m/s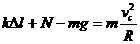
 N
N <
<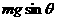
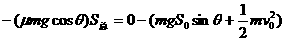
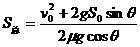
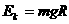 ①
①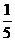 ,故每次与档板碰后动能都是碰前的
,故每次与档板碰后动能都是碰前的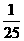 ,物块经过两次与档板碰后动能为
,物块经过两次与档板碰后动能为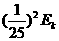 ,根据机械能守恒定律有
,根据机械能守恒定律有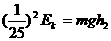 ②
②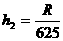 ③
③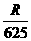 远小于
远小于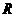 ,此后物块在圆形轨道上的运动都可看成简谐运动,周期
,此后物块在圆形轨道上的运动都可看成简谐运动,周期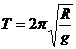 ④
④ ⑤
⑤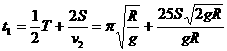 ⑥
⑥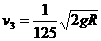 ⑦
⑦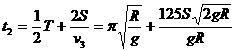 ⑧
⑧ ⑨
⑨