3、在液体中下落的物体最终会达到一个恒定的速度,称之为收尾速度。一个半径为r的球体在液体中下落的收尾速度为v = r2(ρ-ρ/),其中η、g、ρ、ρ/分别为液体的粘滞系数(与液体种类相关的常数)、重力加速度(本题中为已知量)、球体的密度、液体的密度。某同学为了测定某已知密度的液体的粘滞系数,选定了下列器材:一只1000mL的量筒;一块秒表;一把刻度尺;直径不同的铝球若干个(最大直径约10.00mm)。
⑴请列出该同学漏选的器材: 。
⑵实验时,该同学首先将直径约10.00mm的铝球重复从装满被测液体的量筒液面上自由落下测定它通过量筒刻线750mL到500mL和450mL到200mL的两段时间,列表如下:
|
距离L(mL) |
时间t(s) |
平均时间t/(s) |
|
750-500 |
1.74 1.72 1.72 |
1.73 |
|
450-200 |
1.73 1.72 1.73 |
1.73 |
由以上测量数据得到的结论是 。
⑶若测出了不同半径的铝球的收尾速度,要求出液体的粘滞系数,对以上数据应如何处理?
答案:⑴螺旋测微器(或游标卡尺)
⑵在750mm刻度线以内,铝球做匀速运动。
⑶作出v-r2的图象,由图线的斜率求粘滞系数(或先由不同直径铝球对应的收尾速度用公式求出粘滞系数,再求平均值)。
2、学过单摆的周期公式以后,物理兴趣小组的同学们对钟摆产生了兴趣,老师建议他们先研究用厚度和质量分布均匀的方木块(如一把米尺)做成的摆(这种摆被称为复摆),如图所示。让其在竖直平面内做小角度摆动,C点为重心,板长为L,周期用T表示。
甲同学猜想:复摆的周期应该与板的质量有关。
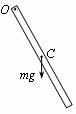 乙同学猜想:复摆的摆长应该是悬点到重心的距离L/2。
乙同学猜想:复摆的摆长应该是悬点到重心的距离L/2。
丙同学猜想:复摆的摆长应该大于L/2。理由是:若OC段看成细线,线栓在C处,C点以下部分的重心离O点的距离显然大于L/2。
为了研究以上猜想是否正确,同学们进行了下面的实验探索:
(1)把两个相同的木板完全重叠在一起,用透明胶(质量不计)粘好,测量其摆动周期,发现与单个木板摆动时的周期相同,重做多次仍有这样的特点。则证明了甲同学的猜想是_______错误______ 的(选填“正确”或“错误”)。
(2)用T0表示板长为L的复摆看成摆长为L/2单摆的周期计算值(T0=2 ),用T表示板长为L复摆的实际周期测量值。计算与测量的数据如下表:
),用T表示板长为L复摆的实际周期测量值。计算与测量的数据如下表:
|
板长L/cm |
25 |
50 |
80 |
100 |
120 |
150 |
|
周期计算值T0/s |
0.70 |
1.00 |
1.27 |
1.41 |
1.55 |
1.73 |
|
周期测量值T/s |
0.81 |
1.16 |
1.47 |
1.64 |
1.80 |
2.01 |
由上表可知,复摆的等效摆长 大于 L/2(选填“大于”、“小于”或“等于”)。
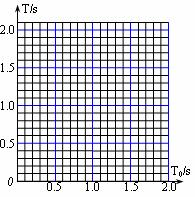
(3)为了进一步定量研究,同学们用描点作图法对数据进行处理,所选坐标如图。请在坐标纸上作出T-T0图,并根据图象中反映出的规律求出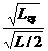 =_________1.16_(结果保留三位有效数字,其中L等是板长为L时的等效摆长T=2
=_________1.16_(结果保留三位有效数字,其中L等是板长为L时的等效摆长T=2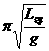 )。
)。
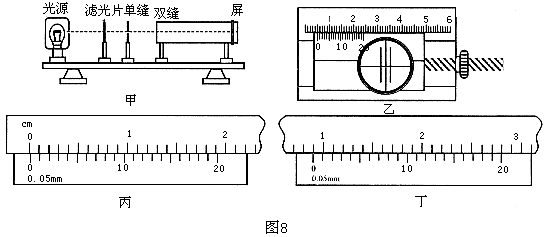 答案: 0.15; 8.95;
答案: 0.15; 8.95; 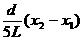 ;
; 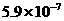 ;
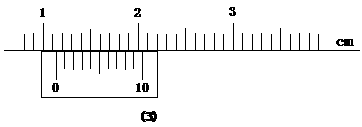
;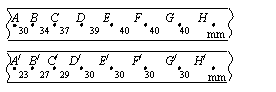 已知电动玩具小车在水平面上运动过程所受阻力与速度成正比。接通电源后小车的电动机以额定功率运转。为测定该电动机的额定功率,首先用弹簧秤以2.0N的水平恒力,拉动小车沿水平面运动,小车尾部夹有纸带,运动过程中打点计时器打出的部分纸带如右上图所示;然后换掉纸带,接通小车的电动机,电动机以额定功率工作,让小车仍在该水平面上运动,打点计时器打出的部分纸带如右下图所示。(两图中每相邻两个计数点之间都还有打点计时器打下的4个点未画出,电源频率为50Hz。相邻计数点间的距离已标在图上,单位mm。)由以上两步操作可知:小车所受阻力大小与速度大小的比例系数为 __ ;小车上电动机的额定功率为 。
已知电动玩具小车在水平面上运动过程所受阻力与速度成正比。接通电源后小车的电动机以额定功率运转。为测定该电动机的额定功率,首先用弹簧秤以2.0N的水平恒力,拉动小车沿水平面运动,小车尾部夹有纸带,运动过程中打点计时器打出的部分纸带如右上图所示;然后换掉纸带,接通小车的电动机,电动机以额定功率工作,让小车仍在该水平面上运动,打点计时器打出的部分纸带如右下图所示。(两图中每相邻两个计数点之间都还有打点计时器打下的4个点未画出,电源频率为50Hz。相邻计数点间的距离已标在图上,单位mm。)由以上两步操作可知:小车所受阻力大小与速度大小的比例系数为 __ ;小车上电动机的额定功率为 。
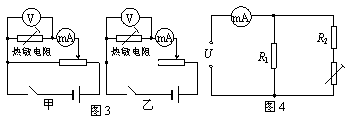
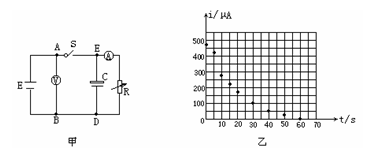 C.断开开关S,同时开始计时,每隔5s测读一次电流i的值,将测得数据填入表格,并标示在图乙的坐标纸上(时间t为横坐标,电流i为纵坐标),如图乙中小黑点所示。
C.断开开关S,同时开始计时,每隔5s测读一次电流i的值,将测得数据填入表格,并标示在图乙的坐标纸上(时间t为横坐标,电流i为纵坐标),如图乙中小黑点所示。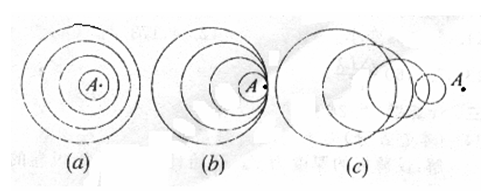
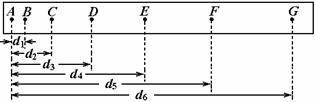 (1)计算vF的公式为vF=____;
(2)根据(1)中得到的数据,以A点对应的时刻为t=0,
(1)计算vF的公式为vF=____;
(2)根据(1)中得到的数据,以A点对应的时刻为t=0, 试在图中所给的坐标系中,作出v-t图象,并求物体的
试在图中所给的坐标系中,作出v-t图象,并求物体的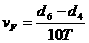 (2)a=0.425±0.005m/s2 图略(3)偏小
(2)a=0.425±0.005m/s2 图略(3)偏小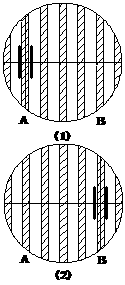

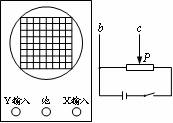 如图是《练习使用示波器》实验的示意图,图中“X输入”、“Y输入”、“地”为信号输入接线柱。实验要求用示波器测右图b、c间的直流电压。把b接“地”接线柱,欲使P滑动时,亮斑在竖直方向移动,则c端应接 Y输入 接线柱。实验发现,当P滑到最左端时,亮斑恰好在荧光屏的中心;当P滑到最右端时,亮斑向下偏离中心3.0格。当P滑到某点时,亮斑向下偏离中心2.5格,则此时b、c间的电压为
1.25 V。(图中电源是电动势为1.5V,内阻不计的一节干电池)
如图是《练习使用示波器》实验的示意图,图中“X输入”、“Y输入”、“地”为信号输入接线柱。实验要求用示波器测右图b、c间的直流电压。把b接“地”接线柱,欲使P滑动时,亮斑在竖直方向移动,则c端应接 Y输入 接线柱。实验发现,当P滑到最左端时,亮斑恰好在荧光屏的中心;当P滑到最右端时,亮斑向下偏离中心3.0格。当P滑到某点时,亮斑向下偏离中心2.5格,则此时b、c间的电压为
1.25 V。(图中电源是电动势为1.5V,内阻不计的一节干电池)