摘要：23．(命题人:如东中学何鹏.审题人:如东中学缪林.由2008年广东省韶关市高三摸底考试数学 设函数的定义域为R.当x＜0时＞1.且对任意的实数x.y∈R.有． (Ⅰ)求.判断并证明函数的单调性, (Ⅱ)数列满足.且． ①求通项公式． ②当时.不等式对不小于2的正整数恒成立.求x的取值范围． [解析](Ⅰ)时.f(x)＞1． 令x＝-1.y＝0.则f(-1)＝f．∵f(-1)＞1 .∴f(0)＝1． 若x＞0.则f(x-x)＝f(0)＝f(x)f(-x)． 故.故x∈R. f(x)＞0． 任取x1＜x2.. .故f(x)在R上减函数． (Ⅱ)①．由f(x)单调性.an+1＝an+2 . 故{an}等差数列.． ②． ∴是递增数列． 当n≥2时.. . 即． 而a＞1.∴x＞1.故x的取值范围．
网址：http://m.1010jiajiao.com/timu3_id_533645[举报]
在一次数学考试中，第21题和第22题为选做题．规定每位考生必须且只须在其中选做一题．设4名考生选做每一道题的概率均为
．
（1）求其中甲、乙两名学生选做同一道题的概率；
（2）设这4名考生中选做第22题的学生个数为ξ，求ξ的概率分布及数学期望． 查看习题详情和答案>>
| 1 | 2 |
（1）求其中甲、乙两名学生选做同一道题的概率；
（2）设这4名考生中选做第22题的学生个数为ξ，求ξ的概率分布及数学期望． 查看习题详情和答案>>
第Ⅰ小题：已知函数f（x）=x+1，设g1（x）=f（x），gn（x）=f（gn-1（x））（n＞1，n∈N*）
（1）求g2（x），g3（x）的表达式，并猜想gn（x）（n∈N*）的表达式（直接写出猜想结果 ）
（2）若关于x的函数y=x2+
gi(x)(n∈N*)在区间(-∞，-
]上的最小值为6，求n的值．
第Ⅱ小题：设关于x的不等式lg（|x+3|+|x-7|）＞a
（1）当a=1时，解这个不等式；（2）当a为何值时，这个不等式的解集为R．
查看习题详情和答案>>
（1）求g2（x），g3（x）的表达式，并猜想gn（x）（n∈N*）的表达式（直接写出猜想结果 ）
（2）若关于x的函数y=x2+
| n |
 |
| i=1 |
| 1 |
| 2 |
第Ⅱ小题：设关于x的不等式lg（|x+3|+|x-7|）＞a
（1）当a=1时，解这个不等式；（2）当a为何值时，这个不等式的解集为R．
. (本小题满分14分)
第21题
设双曲线
=1( a > 0, b > 0 )的右顶点为A，P是双曲线上异于顶点的一个动点，从A引双曲线的两条渐近线的平行线与直线OP分别交于Q和R两点.
(1) 证明：无论P点在什么位置，总有|
|2 = |
·
| ( O为坐标原点)；
(2) 若以OP为边长的正方形面积等于双曲线实、虚轴围成的矩形面积，求双曲线离心率的取值范围；
查看习题详情和答案>>
.
，求
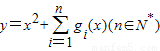在区间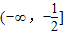
上的最小值为6，求n的值．