题目内容
在一次数学考试中,第21题和第22题为选做题.规定每位考生必须且只须在其中选做一题.设4名考生选做每一道题的概率均为| 1 | 2 |
(1)求其中甲、乙两名学生选做同一道题的概率;
(2)设这4名考生中选做第22题的学生个数为ξ,求ξ的概率分布及数学期望.
分析:(1)设事件A表示“甲选做第21题”,事件B表示“乙选做第21题”,进而分析可得,甲、乙2名学生选做同一道题的事件为“AB+
”,且事件A、B相互独立,由互斥事件的概率计算方法,可得答案;
(2)根据题意,分析可得随机变量ξ的可能取值为0,1,2,3,4,且ξ~B(4,
),进而可得分步列,计算可得答案.
. |
| A |
. |
| B |
(2)根据题意,分析可得随机变量ξ的可能取值为0,1,2,3,4,且ξ~B(4,
| 1 |
| 2 |
解答:解:(1)设事件A表示“甲选做第21题”,事件B表示“乙选做第21题”,
则“甲选做第22题”为
,“甲选做第22题”为
,
进而可得,甲、乙2名学生选做同一道题的事件为“AB+
”,且事件A、B相互独立.
∴P(AB+
)=P(A)P(B)+P(
)P(
)=
×
+(1-
)×(1-
)=
;
(2)随机变量ξ的可能取值为0,1,2,3,4,且ξ~B(4,
).
∴P(ξ=k)=
(
)k(1-
)4-k=
(k=0,1,2,3,4)
∴变量ξ的分布列为:
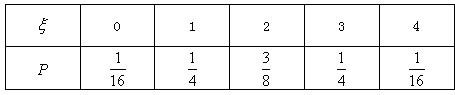 Eξ=0×
Eξ=0×
+1×
+2×
+3×
+4×
=2(或Eξ=np=4×
=2).
则“甲选做第22题”为
. |
| A |
. |
| B |
进而可得,甲、乙2名学生选做同一道题的事件为“AB+
. |
| A |
. |
| B |
∴P(AB+
. |
| A |
. |
| B |
. |
| A |
. |
| B |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)随机变量ξ的可能取值为0,1,2,3,4,且ξ~B(4,
| 1 |
| 2 |
∴P(ξ=k)=
| C | k 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | k 4 |
(
|
∴变量ξ的分布列为:
 Eξ=0×
Eξ=0×| 1 |
| 16 |
| 1 |
| 4 |
| 3 |
| 8 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 2 |
点评:本题考查对立事件、相互独立事件、互斥事件的概率的计算及分步列的运用,有一定的综合性,需要加强学生的这方面的训练.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
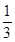 ,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.
,每位学生对每题的选择是相互独立的,各学生的选择相互之间没有影响.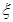 ,求
,求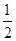 .
. ,求
,求