题目内容
第Ⅰ小题:已知函数f(x)=x+1,设g1(x)=f(x),gn(x)=f(gn-1(x))(n>1,n∈N*)(1)求g2(x),g3(x)的表达式,并猜想gn(x)(n∈N*)的表达式(直接写出猜想结果 )
(2)若关于x的函数
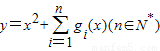 在区间
在区间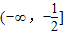 上的最小值为6,求n的值.
上的最小值为6,求n的值.第Ⅱ小题:设关于x的不等式lg(|x+3|+|x-7|)>a
(1)当a=1时,解这个不等式;(2)当a为何值时,这个不等式的解集为R.
【答案】分析:第Ⅰ小题:(1)根据题意g1(x)=f(x)=x+1,gn(x)=f(gn-1(x)),令n=2求出g2(x)的表达式;由g2(x),gn(x)=f(gn-1(x)),令n=2求出g3(x)的表达式,观察求出的表达式g1(x),g2(x)及g3(x),发现其规律为n等于几,其解析式为x加几,根据猜想写出gn(x)的表达式即可;
(2)把(1)中猜想出的gn(x)的表达式代入到函数解析式中,根据等差数列的求和公式化简,得到y与x成二次函数关系,根据二次函数求最值的方法表示出y的最大值,让其等于6列出关于n的方程,求出方程的解即可得到n的值;
第Ⅱ小题:(1)把a=1代入不等式,由对数的运算性质化简后,讨论x的取值化简绝对值不等式,即可求出不等式的解集;
根据|x+a|+|x+b|≥|(x+a)-(x+b)|求出|x+3|+|x-7|的最小值,进而根据底数为10的对数为增函数,求出lg((|x+3|+|x-7|)的最小值,让a小于求出的最小值即可得到a的取值范围.
解答:解:第Ⅰ小题:(1)∵g1(x)=f(x)=x+1,
∴g2(x)=f(g1(x))=f(x+1)=(x+1)+1=x+2,
g3(x)=f(g2(x))=f(x+2)=(x+2)+1=x+3,
∴猜想gn(x)=x+n;
(2)∵gn(x)=x+n,
∴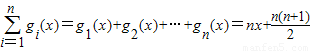 ,
,
∴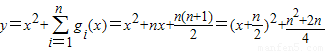 ,
,
∵n>1,n∈N*,∴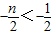 ,
,
又∵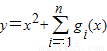 在区间
在区间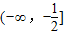 上的最小值为6,
上的最小值为6,
当 时,
时,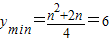 ,解得n=4;
,解得n=4;
第Ⅱ小题:(1)由题意得:|x+3|+|x-7|>10,解得:x<-3或x>7;
(2)∵|x+3|+|x-7|的最小值为10,
∴lg(|x+3|+|x-7|)的最小值为1
要使不等式的解集为R,则须a<1.
点评:此题考查了绝对值不等式的解法,二次函数的性质及对数函数的单调性,考查了学生观察条件,作出猜想,归纳总结的能力.归纳总结得到gn(x)的表达式是解第一问的突破点;在解第二问时注意运用|x+a|+|x+b|≥|(x+a)-(x+b)|这个性质.
(2)把(1)中猜想出的gn(x)的表达式代入到函数解析式中,根据等差数列的求和公式化简,得到y与x成二次函数关系,根据二次函数求最值的方法表示出y的最大值,让其等于6列出关于n的方程,求出方程的解即可得到n的值;
第Ⅱ小题:(1)把a=1代入不等式,由对数的运算性质化简后,讨论x的取值化简绝对值不等式,即可求出不等式的解集;
根据|x+a|+|x+b|≥|(x+a)-(x+b)|求出|x+3|+|x-7|的最小值,进而根据底数为10的对数为增函数,求出lg((|x+3|+|x-7|)的最小值,让a小于求出的最小值即可得到a的取值范围.
解答:解:第Ⅰ小题:(1)∵g1(x)=f(x)=x+1,
∴g2(x)=f(g1(x))=f(x+1)=(x+1)+1=x+2,
g3(x)=f(g2(x))=f(x+2)=(x+2)+1=x+3,
∴猜想gn(x)=x+n;
(2)∵gn(x)=x+n,
∴
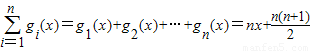 ,
,∴
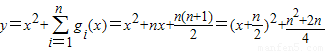 ,
,∵n>1,n∈N*,∴
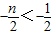 ,
,又∵
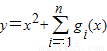 在区间
在区间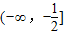 上的最小值为6,
上的最小值为6,当
 时,
时,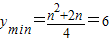 ,解得n=4;
,解得n=4;第Ⅱ小题:(1)由题意得:|x+3|+|x-7|>10,解得:x<-3或x>7;
(2)∵|x+3|+|x-7|的最小值为10,
∴lg(|x+3|+|x-7|)的最小值为1
要使不等式的解集为R,则须a<1.
点评:此题考查了绝对值不等式的解法,二次函数的性质及对数函数的单调性,考查了学生观察条件,作出猜想,归纳总结的能力.归纳总结得到gn(x)的表达式是解第一问的突破点;在解第二问时注意运用|x+a|+|x+b|≥|(x+a)-(x+b)|这个性质.

练习册系列答案
相关题目

 ,直线
,直线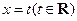
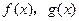 的图象分别交于M、N两点.
的图象分别交于M、N两点. 时,求|MN|的值;
时,求|MN|的值;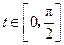 时的最大值.
时的最大值.