��Ŀ����
�ڢ�С�⣺��֪����f��x��=x+1����g1��x��=f��x����gn��x��=f��gn-1��x������n��1��n��N*��
��1����g2��x����g3��x���ı���ʽ��������gn��x����n��N*���ı���ʽ��ֱ��д�������� ��
��2��������x���y=x2+
gi(x)(n��N*)������(-�ޣ�-
]�ϵ���СֵΪ6����n��ֵ��
�ڢ�С�⣺�����x�IJ���ʽlg��|x+3|+|x-7|����a
��1����a=1ʱ�����������ʽ����2����aΪ��ֵʱ���������ʽ�Ľ⼯ΪR��
��1����g2��x����g3��x���ı���ʽ��������gn��x����n��N*���ı���ʽ��ֱ��д�������� ��
��2��������x���y=x2+
| n |
 |
| i=1 |
| 1 |
| 2 |
�ڢ�С�⣺�����x�IJ���ʽlg��|x+3|+|x-7|����a
��1����a=1ʱ�����������ʽ����2����aΪ��ֵʱ���������ʽ�Ľ⼯ΪR��
�������ڢ�С�⣺��1����������g1��x��=f��x��=x+1��gn��x��=f��gn-1��x��������n=2���g2��x���ı���ʽ����g2��x����gn��x��=f��gn-1��x��������n=2���g3��x���ı���ʽ���۲�����ı���ʽg1��x����g2��x����g3��x�������������Ϊn���ڼ��������ʽΪx�Ӽ������ݲ���д��gn��x���ı���ʽ���ɣ�
��2���ѣ�1���в������gn��x���ı���ʽ���뵽��������ʽ�У����ݵȲ����е����ʽ���õ�y��x�ɶ��κ�����ϵ�����ݶ��κ�������ֵ�ķ�����ʾ��y�����ֵ���������6�г�����n�ķ��̣�������̵Ľ⼴�ɵõ�n��ֵ��
�ڢ�С�⣺��1����a=1���벻��ʽ���ɶ������������ʻ��������x��ȡֵ�������ֵ����ʽ�������������ʽ�Ľ⼯��
����|x+a|+|x+b|��|��x+a��-��x+b��|���|x+3|+|x-7|����Сֵ���������ݵ���Ϊ10�Ķ���Ϊ�����������lg����|x+3|+|x-7|������Сֵ����aС���������Сֵ���ɵõ�a��ȡֵ��Χ��
��2���ѣ�1���в������gn��x���ı���ʽ���뵽��������ʽ�У����ݵȲ����е����ʽ���õ�y��x�ɶ��κ�����ϵ�����ݶ��κ�������ֵ�ķ�����ʾ��y�����ֵ���������6�г�����n�ķ��̣�������̵Ľ⼴�ɵõ�n��ֵ��
�ڢ�С�⣺��1����a=1���벻��ʽ���ɶ������������ʻ��������x��ȡֵ�������ֵ����ʽ�������������ʽ�Ľ⼯��
����|x+a|+|x+b|��|��x+a��-��x+b��|���|x+3|+|x-7|����Сֵ���������ݵ���Ϊ10�Ķ���Ϊ�����������lg����|x+3|+|x-7|������Сֵ����aС���������Сֵ���ɵõ�a��ȡֵ��Χ��
����⣺�ڢ�С�⣺��1����g1��x��=f��x��=x+1��
��g2��x��=f��g1��x����=f��x+1��=��x+1��+1=x+2��
g3��x��=f��g2��x����=f��x+2��=��x+2��+1=x+3��
�����gn��x��=x+n��
��2����gn��x��=x+n��
��
gi(x)=g1(x)+g2(x)+��+gn(x)=nx+
��
��y=x2+
gi(x)=x2+nx+
=(x+
)2+
��
��n��1��n��N*����-
��-
��
�֡�y=x2+
gi(x)������(-�ޣ�-
]�ϵ���СֵΪ6��
��x=-
ʱ��ymin=
=6�����n=4��
�ڢ�С�⣺��1��������ã�|x+3|+|x-7|��10����ã�x��-3��x��7��
��2����|x+3|+|x-7|����СֵΪ10��
��lg��|x+3|+|x-7|������СֵΪ1
Ҫʹ����ʽ�Ľ⼯ΪR������a��1��
��g2��x��=f��g1��x����=f��x+1��=��x+1��+1=x+2��
g3��x��=f��g2��x����=f��x+2��=��x+2��+1=x+3��
�����gn��x��=x+n��
��2����gn��x��=x+n��
��
| n |
 |
| i=1 |
| n(n+1) |
| 2 |
��y=x2+
| n |
 |
| i=1 |
| n(n+1) |
| 2 |
| n |
| 2 |
| n2+2n |
| 4 |
��n��1��n��N*����-
| n |
| 2 |
| 1 |
| 2 |
�֡�y=x2+
| n |
 |
| i=1 |
| 1 |
| 2 |
��x=-
| n |
| 2 |
| n2+2n |
| 4 |
�ڢ�С�⣺��1��������ã�|x+3|+|x-7|��10����ã�x��-3��x��7��
��2����|x+3|+|x-7|����СֵΪ10��
��lg��|x+3|+|x-7|������СֵΪ1
Ҫʹ����ʽ�Ľ⼯ΪR������a��1��
���������⿼���˾���ֵ����ʽ�Ľⷨ�����κ��������ʼ����������ĵ����ԣ�������ѧ���۲��������������룬�����ܽ�������������ܽ�õ�gn��x���ı���ʽ�ǽ��һ�ʵ�ͻ�Ƶ㣻�ڽ�ڶ���ʱע������|x+a|+|x+b|��|��x+a��-��x+b��|������ʣ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
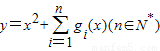 ������
������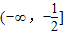 �ϵ���СֵΪ6����n��ֵ��
�ϵ���СֵΪ6����n��ֵ�� ��ֱ��
��ֱ��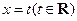
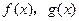 ��ͼ��ֱ���M��N���㣮
��ͼ��ֱ���M��N���㣮 ʱ�����MN����ֵ��
ʱ�����MN����ֵ��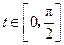 ʱ�����ֵ��
ʱ�����ֵ��