摘要:20. 已知椭圆.直线与椭圆交于.两点.是线段的中点.连接并延长交椭圆于点. (Ⅰ)设直线与直线的斜率分别为..且.求椭圆的离心率的取值范围. (Ⅱ)若直线经过椭圆的右焦点.且四边形是面积为的平行四边形.求直线倾斜角的大小. 如果正数数列满足:对任意的正数M.都存在正整数.使得.则称数列是一个无界正数列. (Ⅰ)若. 分别判断数列.是否为无界正数列.并说明理由, (Ⅱ)若.是否存在正整数.使得对于一切.有成立, (Ⅲ)若数列是单调递增的无界正数列.求证:存在正整数.使得. 湖北省黄冈中学2009届高三五月适应性考试(B卷)
网址:http://m.1010jiajiao.com/timu3_id_533440[举报]
(本题满分13分) 已知椭圆![]() 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过![]() 、
、![]() 、
、![]() 三点. (1)求椭圆
三点. (1)求椭圆![]() 的方程:(2)若点D为椭圆
的方程:(2)若点D为椭圆![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,
的任意一点,![]() ,当
,当![]() 内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线
内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,证明直线
两点,证明直线![]() 与直线
与直线![]() 的交点在定直线上并求该直线的方程.
的交点在定直线上并求该直线的方程.
(本题满分13分) 已知椭圆 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过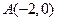 、
、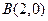 、
、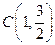 三点. (1)求椭圆
三点. (1)求椭圆 的方程:(2)若点D为椭圆
的方程:(2)若点D为椭圆 上不同于
上不同于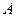 、
、 的任意一点,
的任意一点, ,当
,当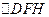 内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线
内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线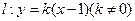 与椭圆
与椭圆 交于
交于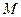 、
、 两点,证明直线
两点,证明直线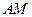 与直线
与直线 的交点在定直线上并求该直线的方程.
的交点在定直线上并求该直线的方程.
 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过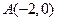 、
、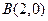 、
、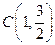 三点. (1)求椭圆
三点. (1)求椭圆 的方程:(2)若点D为椭圆
的方程:(2)若点D为椭圆 上不同于
上不同于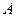 、
、 的任意一点,
的任意一点, ,当
,当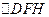 内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线
内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线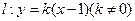 与椭圆
与椭圆 交于
交于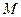 、
、 两点,证明直线
两点,证明直线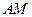 与直线
与直线 的交点在定直线上并求该直线的方程.
的交点在定直线上并求该直线的方程.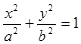 (
(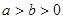 )过点
)过点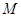 (0,2),离心率
(0,2),离心率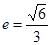 .
.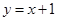 与椭圆相交于
与椭圆相交于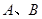 两点,求
两点,求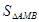 .
.
 的离心率为
的离心率为 ,椭圆短轴长为
,椭圆短轴长为 .
.  的方程;
的方程; 与椭圆
与椭圆 、
、 两点. ①若线段
两点. ①若线段 中点的横坐标为
中点的横坐标为 ,求斜率
,求斜率 的值;②若点
的值;②若点 ,求证:
,求证: 为定值。
为定值。