题目内容
(本题满分13分) 已知椭圆
的中心在坐标原点，焦点在坐标轴上，且经过
、
、
三点. （1）求椭圆的方程：（2）若点D为椭圆上不同于
、
的任意一点，
，当
内切圆的面积最大时。求内切圆圆心的坐标；（3）若直线
与椭圆交于
、
两点，证明直线
与直线
的交点在定直线上并求该直线的方程．
(Ⅰ) 
(Ⅱ) 
（Ⅲ）
解析:
：（1）设椭圆方程为
将
、
、
代入椭圆E的方程，得
解得
.∴椭圆
的方程（4分）
（2）
，设
边上的高为
当点
在椭圆的上顶点时，
最大为
，所以
的最大值为．设的内切圆的半径为
，因为的周长为定值6．所以
，所以的最大值为
．所以内切圆圆心的坐标为 10分
（3）将直线
代入椭圆的方程并整理．得
．设直线
与椭圆的交点
，
由根系数的关系，得
．
直线
的方程为：
，它与直线的交点坐标为
同理可求得直线
与直线的交点坐标为
．
下面证明
、
两点重合，即证明、两点的纵坐标相等：
，
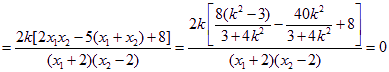
因此结论成立．综上可知．直线与直线的交点住直线上．
练习册系列答案
相关题目
，
，
. 
，
； (2) 若
，求
的取值范围.
的三个内角
依次成等差数列．
，试判断
，求
中，
，
，
分别为内角
，
，
所对的边，且满足
．
，且
，
，求
的值．
展开式中，求：
平面ABCD，AD//BC//FE，AB
AD.
？若存在，试确定点M的位置；若不存在，请说明理由.